Vous apprenez à programmer et vous cherchez à développer vos compétences en algorithmique ? C’est très bien car la création d’algorithmes est le cœur du métier de développeur.
Objectif de cet article
Dans ce billet vous allez apprendre à concevoir un algorithme à partir de zéro.
Vous allez suivre mon raisonnement de A à Z pour résoudre un exercice moyennement difficile : l’exercice 3 de la saison 15 de la BattleDev, un concours de programmation.
Au travers de cet exemple très concret, vous apprendrez à penser comme un développeur en étant en quelque sorte dans mon cerveau pendant que je résous l’exercice.
L’objectif est d’utiliser un cas pratique comme exemple pour illustrer les différentes phases théoriques de la construction d’un algorithme.
Je vais vous enseigner une méthode simple et structurée que vous pourrez appliquer à n’importe quel problème algorithmique pour le résoudre.
Dès maintenant, vous pouvez télécharger tous les algorithmes et leur implémentation en JavaScript (fichier ZIP) qu’on va créer dans ce billet pour les modifier à votre guise.
Notez que j’ai utilisé des instructions de base (boucles classiques, affectations simples etc.) pour l’implémentation en JavaScript car cet article s’adresse aux débutants en programmation.
Je veux montrer que même avec les outils de base du langage on peut déjà résoudre des exercices complexes. Vous ne trouverez donc pas de destructuring, de fonctions fléchées, ni de map(), filter(), reduce() et autres joyeusetés dans mon code, c’est fait exprès !
Merci donc de vous abstenir de me dire que je peux rédiger mon code de façon plus concise et plus moderne, je le sais ! Mais ce n’est pas l’objectif ici 😘.
Si vous voulez aller plus loin, je vous invite à suivre le module algorithmique de ma formation JavaScript. Vous y apprendrez à rédiger du pseudo-code pour structurer votre pensée et résoudre des problèmes de plus en plus complexes. Rassurez-vous on commencera avec des problèmes bien plus faciles que celui que je vous présente ici !
Sommaire
- Définitions
- Prérequis
- Énoncé de l’exercice
- Phase 0 : analyse de l’énoncé
- Phase 1 : simplification du problème
- Phase 2 : exploration du problème
- Phase 3 : augmentez la difficulté
- La méthode pour rédiger un algorithme
- Une question de temps et d’itérations
- Le mot de la fin
- Conclusion
Définitions
Avant de commencer, un petit point de vocabulaire : on dit algorithmique, pas algorithmie. Ce dernier terme est désuet. L’étude des algorithmes s’appelle l’algorithmique.
Mais qu’est-ce que l’algorithmique au juste ?
L’algorithmique c’est le domaine de l’étude et de la conception d’algorithmes.
C’est l’art de savoir décomposer un problème en sous-parties pour produire une solution à celui-ci sous la forme d’un algorithme.
Autrement dit c’est l’art de savoir écrire la recette de cuisine qu’il faut suivre pour résoudre un problème donné.
Dernier point de vocabulaire : implémenter signifie rédiger dans un langage de programmation un algorithme donné. On transforme le pseudo-code de l’algorithme en code source en utilisant la syntaxe du langage de programmation choisi.
Prérequis
Vous aurez besoin d’avoir des notions de base en programmation (peu importe le langage) : savoir ce qu’est une variable, une boucle, une condition, une fonction.
Je vous invite à lire cet article en plusieurs fois car il est très riche et très dense et vous allez devoir vous concentrer pendant une longue période pour tout assimiler.
J’ai mis plusieurs semaines pour le rédiger et tout expliquer en détails, donc n’hésitez pas à prendre votre temps pour lire chaque partie et faites des pauses !
Énoncé de l’exercice
Vous pouvez trouver l’énoncé de l’exercice sur le site isograd, sélectionnez dans la liste des exercices celui intitulé 25 heures sur 25.
Je vous remets l’énoncé ci-dessous des fois que la source ne disparaisse :
Difficile de trouver un moment libre dans l’agenda de tous vos collègues pour organiser vos réunions d’équipe ! Vous décidez de leur demander de vous communiquer les créneaux où ils sont indisponibles. En utilisant ces données, votre objectif est de trouver un créneau de 60 minutes consécutives qui conviendra à tout le monde pendant la semaine à venir.
Données d’entrée
Ligne 1 : un entier N compris entre 1 et 1000 représentant le nombre de créneaux impossibles pour la réunion
Lignes 2 à N + 1 : un créneau impossible pour un collègue au format jour hh:mm-hh:mm. Le jour est au format ISO : 1 = lundi, 2 = mardi, etc. Les minutes de début et de fin sont incluses dans l’indisponibilité. Les horaires de travail sont du lundi au vendredi de 8:00 à 17:59. Les créneaux impossibles sont inclus dans les horaires de travail de votre entreprise.
Sortie
Une ligne au format jour hh:mm-hh:mm représentant l’horaire de réunion choisi.
Il doit être :
- Pendant les horaires de travail, sans les dépasser
- D’une durée d’exactement 60 minutes
- Les minutes de début et de fin sont incluses dans l’horaire donc une réunion de 08:00 à 8:59 ou de 9:20 à 10:19 font exactement 60 minutes
- N’être en intersection avec aucun créneau impossible d’aucun collègue
- Il est garanti qu’il existe au moins une solution. S’il en existe plusieurs, vous pouvez donner n’importe quel horaire valide.
Exemple
Quelques rappels :
- La 1ère ligne des données d’entrée représente le nombre de créneaux impossibles pour la réunion
- Le premier chiffre des lignes suivantes est le numéro du jour (1 = lundi, 2 = mardi, … 5 = vendredi)
Pour l’entrée :
5 1 08:45-12:59 3 11:09-11:28 5 09:26-09:56 5 16:15-16:34 3 08:40-10:12
Une solution possible est :
1 13:00-13:59
En effet, le premier jour il n’y a qu’un seul créneau impossible de 08:45 à 12:59. En faisant par exemple commencer la réunion à 13:00 et en la terminant à 13:59, elle n’aura aucune intersection avec les créneaux impossibles. Il existe par ailleurs de nombreuses autres solutions par exemple n’importe quel intervalle de 60 minutes durant les horaires de travail du jour 2.
Phase 0 : analyse de l’énoncé
Première chose à faire lorsqu’on lit un énoncé d’exercice de programmation, il faut l’analyser pour bien le comprendre et noter les points importants à garder en tête quand on rédige l’algorithme.
Voici les points importants à retenir sur cet énoncé :
- Les minutes de début et de fin sont incluses dans l’horaire donc une réunion de 08:00 à 08:59 ou de 09:20 à 10:19 fait exactement 60 minutes
- Les horaires de travail sont du lundi au vendredi de 08:00 à 17:59. Les créneaux impossibles sont inclus dans les horaires de travail de votre entreprise.
Reprenons chaque point et détaillons-le.
Les minutes de début et de fin sont incluses dans l’horaire donc une réunion de 08:00 à 08:59 ou de 09:20 à 10:19 fait exactement 60 minutes
Première chose, l’énoncé prend le temps de définir comment sont interprétées les bornes d’une indisponibilité. Ce sera très utile pour éviter l’erreur classique en programmation de décalage à 1.
Pour déterminer la durée d’un créneau donné, il faudra inclure les minutes de début et de fin. Autrement dit, comme dans l’exemple de 08:00 à 08:59, on a une durée de 60 minutes et non pas 59 minutes comme on pourrait le supposer à priori.
Donc pour un créneau allant de 08:00 à 08:30, on a 31 minutes et pas 30 minutes.
On peut donc conclure que pour calculer une durée sur un créneau, il faut faire horaireDeFin - horaireDeDebut + 1. Exemple : 08:30 – 08:00 + 1 = 30 + 1 = 31 minutes.
Les horaires de travail sont du lundi au vendredi de 08:00 à 17:59. Les créneaux impossibles sont inclus dans les horaires de travail de votre entreprise.
La journée commence à 08:00 et se termine à 17:59 inclus. Les créneaux impossibles sont inclus dans ces horaires donc ça veut dire que dans la liste des créneaux qu’on nous donne en entrée, le début minimum d’un créneau sera 08:00 et la fin maximum sera 17:59.
C’est pratique pour nous car ça nous évite de devoir vérifier cette condition et/ou ajuster le créneau à ces horaires de début et de fin de journée. On sait tout de suite qu’ils sont cohérents par rapport à la journée de travail.
Analyse de l’exemple
Dans l’exemple d’entrée :
5 1 08:45-12:59 3 11:09-11:28 5 09:26-09:56 5 16:15-16:34 3 08:40-10:12
On peut voir que les créneaux ne se chevauchent pas. Par exemple pour le vendredi (jour 5), on a 09:26-09:56 et 16:15-16:34. Ces créneaux ne se « touchent » pas, ils ne sont pas superposés d’une quelconque façon.
Pourtant, si on regarde les jeux de tests suivants dans cet exercice, on se rend compte qu’ils peuvent l’être ! L’énoncé ne donne en effet aucune indication à ce sujet, donc on peut avoir des créneaux qui se chevauchent.
Par exemple :
2 5 09:30-10:00 5 09:45-16:00
Ici le second créneau 09:45-16:00 est à cheval sur le premier 09:30-10:00. Cela va ajouter de la complexité au problème.
Il faudra prendre en compte ce cas particulier dans notre algorithme.
Phase 1 : simplification du problème
Vous pouvez vous sentir très submergé par la difficulté de cet exercice et ça peut vous tétaniser sur le champ. Rassurez-vous c’est une sensation commune chez les débutants et même chez les développeurs plus expérimentés !
Vous connaissez sûrement la réponse à la question : comment mange-t-on un éléphant ?
Une bouchée à la fois !
Eh bien on va faire exactement ça : on va découper le problème en sous-parties plus petites, moins impressionnantes, qu’on va résoudre une à une puis qu’on va assembler pour former l’algorithme final.
C’est là tout l’art de la simplification d’un problème.
Pour cet exercice, une partie de la difficulté vient du fait qu’on doive gérer des créneaux impossibles pour toute la semaine, soit 5 jours du lundi au vendredi.
Si on est capable de gérer une journée, on sera capable de gérer 5 journées en ajoutant un petit peu de code autour via une boucle par exemple.
Réduisons donc le problème à la gestion d’une seule journée : il faudra trouver un créneau disponible de 60 minutes sur une seule journée et non pas 5.
Pour notre fichier d’entrée, on considérera qu’il ne contient donc que les créneaux du lundi par exemple.
Créons un fichier simple d’entrée pour ce plus petit problème :
4 1 10:45-14:47 1 11:10-12:32 1 08:45-12:59 1 13:50-17:50
Ce fichier d’entrée est encore complexe, en effet il y a des créneaux qui se chevauchent, ça rend l’exercice plus difficile de gérer ce cas particulier.
On pourra trouver un moyen de gérer ces chevauchements plus tard.
Pour l’instant, on va encore simplifier l’exercice en supposant que les horaires ne se chevauchent jamais. Voici donc un nouvel exemple d’entrée :
4 1 10:45-14:47 1 08:30-09:52 1 15:15-16:30 1 16:40-17:10
On voit que c’est déjà plus simple n’est-ce pas ? Si je vous demande de trouver un créneau de 60 minutes dans ce fichier, ça vous semble plus facile que l’énoncé initial non ?
Simplifions-le encore !
Les créneaux ne sont pas dans l’ordre chronologique, ça simplifierait les choses d’avoir tous les créneaux dans l’ordre pour les lire un à un et chercher un trou de 60 minutes entre ceux-ci n’est-ce pas ?
Alors faisons ça avec ce nouveau fichier d’exemple (qui est juste le même que le précédent mais dans l’ordre chronologique) :
4 1 08:30-09:52 1 10:45-14:47 1 15:15-16:30 1 16:40-17:10
Et voilà ! On a classé la liste des horaires dans l’ordre chronologique en utilisant les horaires de début comme référence.
On peut encore le simplifier.
Vu qu’on ne travaille que sur une journée, gérer le numéro du jour est inutile donc on peut le supprimer, ce qui donne :
4 08:30-09:52 10:45-14:47 15:15-16:30 16:40-17:10
On peut encore le simplifier ! On a 4 créneaux impossibles, réduisons ça à un seul créneau impossible :
1 08:30-09:52
C’est tout de suite moins impressionnant hein ! Trouver un créneau de 60 minutes avec ces données d’entrée devrait être faisable !
Alors qu’a-t-on fait jusqu’à présent ?
Eh bien on a simplifié ce problème complexe en retirant tous les cas particuliers et toutes les difficultés sous-jacentes sans en modifier l’essence.
C’est-à-dire sans modifier la nature même du problème donné qui est d’être capable de trouver un créneau disponible de 60 minutes en ayant une contrainte d’horaire.
En fait, la difficulté d’un problème ne vient pas d’une difficulté intrinsèque de celui-ci mais simplement du fait que pour le résoudre, il faudra résoudre plein de petits sous-problèmes à la chaîne !
Et c’est ça qui vous fige parfois avant même d’avoir commencé : vous vous rendez compte de l’étendue des problèmes à résoudre et vous vous sentez submergé ! C’est pour ça qu’il faut simplifier le problème en premier.
Ici on a déjà pu identifier 4 sous-problèmes qu’on a mis de côté pour l’instant :
- Classer dans l’ordre chronologique les créneaux
- Gérer les superpositions d’horaires (chevauchements)
- Gérer les numéros du jour
- Gérer les 5 jours de la semaine et pas juste un seul
Pour simplifier l’exercice on a retiré tous ces sous-problèmes pour se concentrer sur le cœur de celui-ci, sur ce qu’on appelle le cas nominal : trouver un créneau de 60 minutes en prenant en compte un créneau impossible.
Phase 2 : exploration du problème
Maintenant qu’on a atteint le cœur du problème, on va travailler à l’envers.
On va résoudre ce problème relativement simple puis rajouter à chaque fois de la complexité à celui-ci jusqu’à arriver à reproduire l’énoncé de l’exercice.
On dit qu’on va travailler par incrémentation, c’est-à-dire étape par étape.
Lorsqu’on aura une solution qui fonctionne on testera avec un exemple un peu plus complexe et on adaptera notre algorithme pour qu’il prenne en compte cette nouvelle complexité.
Commençons donc avec notre fichier d’entrée simplifié :
1
08:30-09:52
Explorons le problème avec notre cerveau d’humain déjà !
Rappel de notre énoncé simplifié : il faut trouver un créneau de 60 minutes disponible sur cette journée sachant que la journée commence à 08:00 (inclus) et se termine à 17:59 (inclus) et qu’il existe un créneau impossible de 08:30 à 09:52 (ces 2 horaires sont exclus car ils font partie du créneau impossible).
Comment feriez-vous pour résoudre ce problème en mettant de côté tout ce que vous savez de la programmation et de l’algorithmique ?
Instinctivement, vous savez que la réponse possible est tous les créneaux de 60 min à partir de 09:53 ! Donc une réponse possible est 09:53 – 10:52.
Comment avez-vous fait pour trouver cette réponse ? C’est là qu’intervient la phase de rédaction de l’algorithme. Il va falloir décortiquer chaque étape de votre pensée.
Faisons-le ensemble :
- On regarde si entre 08:00 (début de journée, inclus) et 08:30 (exclu) il y a 60 min ? Non.
- On regarde si entre 09:52 (exclu) et la fin de journée à 17:59 (inclus) il y a 60 min ? Oui !
- On s’arrête là et on prend 09:52 + 1 min comme début d’horaire de créneau disponible, soit 09:53.
- On ajoute 59 min et ça donne 10:52.
- Une réponse possible est 09:53-10:52.
Ce n’est pas si compliqué finalement ? Maintenant on va prendre chaque étape et la décortiquer pour en faire un algorithme.
On regarde si entre 08:00 (inclus) et 08:30 (exclu) il y a 60 min ?
Premier bloc de notre algorithme : il faut trouver une façon de calculer la durée d’un « trou » entre 2 horaires donnés. Dans cet exemple, entre 08:00 (inclus car c’est le début de la journée) et 08:30 (exclu car c’est le début d’un horaire impossible).
Pour faciliter les choses, on ne manipulera que des horaires exclus (impossibles) car les données sont majoritairement des horaires exclus (liste des créneaux impossibles).
Par « horaire exclu » j’entends par là des horaires qui ne peuvent pas se trouver dans la réponse finale de l’exercice c’est-à-dire dans les horaires du créneau de 60 min disponible qu’on doit afficher à la fin de notre algorithme.
Par conséquent, on fixera le début de journée à 07:59 et la fin de journée à 18:00. Ainsi les horaires inclus de la journée seront bien 08:00 et 17:59.
Notez que j’ai pris cette décision après avoir eu plein de problèmes pour rédiger la solution finale simplement. Devoir gérer des horaires parfois inclus et parfois exclus est très pénible !
Je suis tombé dans le cas classique des erreurs de décalage à 1. Je me suis rendu compte d’erreurs de logique à la toute fin de mon programme qui ne passait pas certains tests !
La construction d’un algorithme n’est jamais quelque chose de linéaire : on fait des va-et-viens incessants entre le code et l’algorithme, c’est parfaitement normal.
Revenons à notre exemple.
On cherche la durée du trou entre les horaires exclus 07:59 et 08:30, autrement dit on cherche la durée du trou qu’il y a à l’intérieur de l’horaire 07:59-08:30.
Les horaires de ce trou sont donc 08:00-08:29 inclus. On a ajouté 1 minute à 07:59 et on a retranché 1 minute à 08:30 pour trouver le créneau du trou.
Comme on l’a vu précédemment la durée d’un tel créneau se calcule en faisant 08:29 – 08:00 + 1 ce qui vaut 30 minutes.
On peut rédiger une fonction en pseudo-code qui va calculer simplement la durée d’un trou en minutes en se basant sur les horaires exclus qu’on lui passera en paramètres.
On va calculer dans un premier temps la durée entre les 2 horaires exclus, retrancher 2 pour calculer la durée du trou à l’intérieur puis ajouter 1 pour respecter le calcul de durée imposé par l’énoncé, voici un exemple détaillé de la réflexion :
- Soit les horaires 07:59 et 08:30, on doit déterminer la durée du trou à l’intérieur. On calcule la différence : 08:30 – 07:59 = 31 minutes.
- La durée du trou correspondant est égale à cette différence moins 2 minutes. En effet pour trouver les créneaux du trou on ajoute 1 minute à l’horaire de début et on retranche 1 minute à l’horaire de fin, autrement dit on raccourci la durée de 1 + 1 = 2 minutes.
- Pour respecter l’énoncé, il faut maintenant ajouter 1 min à notre durée du trou pour obtenir la durée du trou finale de 08:00 à 08:29 soit 30 minutes.
On peut aller plus vite en disant simplement qu’il suffit de calculer la différence des horaires exclus passés en paramètres et de retrancher 1 pour trouver la durée du trou. J’ai préféré laisser les étapes intermédiaires dans l’algorithme.
Passons à la rédaction de cet algorithme qu’on va appeler dureeTrou.
Notez que la façon d’écrire du pseudo-code n’est pas standardisée, je me suis inspiré de cette convention pour rédiger le pseudo-code de cet article.
Voici la fonction en pseudo-code qui permet de calculer la durée d’un trou en minutes entre 2 horaires donnés. Pour les horaires de 08:15 à 08:30 par exemple elle renverra la valeur 14 (minutes) :
FONCTION dureeTrou(horaireDebut, horaireFin)
PARAMETRES locaux
CHAINE : horaireDebut, horaireFin
VARIABLES
ENTIER : heuresDebut, minutesDebut, heuresFin, minutesFin, duree
DEBUT
// Ex.: horaireDebut vaut "08:15"
heuresDebut ← extraireHeures(horaireDebut)
minutesDebut ← extraireMinutes(horaireDebut)
// Ex.: horaireFin vaut "08:30"
heuresFin ← extraireHeures(horaireFin)
minutesFin ← extraireMinutes(horaireFin)
// On calcule la durée du créneau en minutes
duree ← (heuresFin - heuresDebut) * 60 + (minutesFin - minutesDebut)
// On calcule la durée du trou à l'intérieur de ce créneau
duree ← duree - 2
// On ajuste la durée pour correspondre aux contraintes de l'énoncé
RETOURNER duree + 1
FIN
Vous pouvez télécharger l’algorithme et une implémentation possible de celui-ci en JavaScript (fichiers dureeTrou.algo et dureeTrou.js).
Cet algorithme renverra des valeurs négatives si l’horaire de début est égal à l’horaire de fin ou bien si l’horaire de début se trouve après l’horaire de fin.
Notez que j’utilise 2 fonctions extraireHeures et extraireMinutes qui viennent simplement récupérer respectivement dans la chaîne de caractères « 08:15 » la valeur numérique 8 et la valeur 15.
Lorsqu’on rédige un algorithme, il ne faut pas rentrer dans les petits détails et rester concentré sur l’objectif principal de la fonction qu’on rédige.
Bien évidemment, ces 2 fonctions devront être écrites un moment donné, mais elles sont relativement simples à créer pour ne pas les inclure ici.
Par ailleurs elles seront fortement dépendantes du langage de programmation utilisé pour implémenter l’algorithme.
Par exemple, extraireHeures pourra s’écrire en 1 ligne Number(horaireDebut.split(':')[0]) en JavaScript.
Maintenant qu’on a cette première pièce du puzzle on va pouvoir effectuer les premières étapes de notre réflexion. On va vérifier s’il y a un trou de 60 minutes entre le début de la journée et le premier horaire et entre la fin du premier horaire et la fin de la journée :
ALGORITHME detecterCreneauDisponible-v0
VARIABLES
CHAINE: debutJournee, finJournee, horaireDebut, horaireFin
DEBUT
debutJournee ← "07:59"
finJournee ← "18:00"
horaireDebut ← lireHoraireDebutDuPremierHoraire()
horaireFin ← lireHoraireFinDuPremierHoraire()
// Est-ce qu'il y a un trou d'au moins 60 minutes entre
// le début de journée et le début du premier horaire ?
SI (dureeTrou(debutJournee, horaireDebut) >= 60) ALORS
afficherReponse(debutJournee)
finDuProgramme
FIN SI
// Est-ce qu'il y a un trou d'au moins 60 minutes entre
// la fin du premier horaire et la fin de la journée ?
SI (dureeTrou(horaireFin, finJournee) >= 60) ALORS
afficherReponse(horaireFin)
finDuProgramme
FIN SI
FIN
Vous pouvez télécharger l’algorithme et une implémentation possible de celui-ci en JavaScript (fichiers detecterCreneauDisponibleV0.algo et detecterCreneauDisponibleV0.js).
Plutôt simple comme algorithme non ?
Ici j’ai à nouveau utilisé plusieurs fonctions pour simplifier les choses : lireHoraireDebutDuPremierHoraire, lireHoraireFinDuPremierHoraire, afficherReponse et finDuProgramme.
Leur nom est assez explicite, les 2 premières permettent de lire les horaires de début et de fin respectivement du premier horaire dans le fichier d’entrée.
Ensuite afficherReponse(horaire) permet d’afficher la réponse sous la forme « 09:53-10:52 » et enfin finDuProgramme permet de ne pas exécuter la suite du programme et d’arrêter celui-ci immédiatement.
Toutes ces fonctions permettent de rester concentré sur l’algorithme à rédiger qui est de trouver un créneau disponible.
On peut voir dans cet algorithme qu’on répète un bloc de code très similaire 2 fois de suite. Voici ce bloc écrit de façon un peu plus générale :
SI (dureeTrou(horaireDebut, horaireFin) >= 60) ALORS afficherReponse(horaireDebut) finDuProgramme FIN SI
On se doute qu’à un moment donné il va falloir factoriser ce code d’une façon ou d’une autre…
Stressez votre algorithme avec des cas particuliers : la règle des 3 possibilités
On a pris un exemple avec un cas nominal simple : un seul créneau impossible 08:30-09:52. Bien sûr, même en se limitant à un seul créneau, on peut rencontrer des cas particuliers !
On a rédigé un algorithme qui fonctionne avec cet exemple précis en tête.
Mais est-ce qu’il va fonctionner pour tous les cas possibles et plus spécifiquement pour les cas particuliers ?
Avant de continuer il faut tester que cet algorithme fonctionne aussi pour les cas particuliers qu’on appelle les cas limites (aussi appelés edge cases en anglais).
Ces cas limites se trouvent quasiment tout le temps aux bornes des valeurs possibles qu’on manipulent. Il va donc falloir trouver ces cas particuliers et tester notre algorithme avec ceux-ci.
Trouver les cas particuliers peut parfois être compliqué, mais 99 % du temps il suffit de se reporter à une règle toute simple : la règle des 3 possibilités.
Je vous la fait courte : un ordinateur ne manipule que des nombres car le micro-processeur qui est son cerveau ne fait que des calculs sur des nombres.
La majorité du temps en programmation, on compare des valeurs numériques entre elles pour prendre des décisions dans notre programme.
Même lorsque vous comparez des lettres, en fait, vous comparez des nombres. Chaque lettre correspond à un nombre selon une table de correspondance.
Bref, voici la règle très simple à retenir :
Lorsqu’on compare 2 nombres A et B, il y a toujours 3 possibilités : soit A > B, soit A < B soit A = B.
Simple non ? Si vous comprenez ça, vous venez de faire un pas de géant en algorithmique !
Revenons à nos moutons.
Les créneaux impossibles peuvent varier entre le début de la journée à partir de 08:00 inclus et la fin de journée à 17:59 inclus.
Un créneau impossible est composé de 2 valeurs : un horaire de début et un horaire de fin. On doit donc combiner tout ça en tenant compte des contraintes de l’énoncé :
- l’horaire de fin d’un créneau ne peut pas être avant celle du début de ce créneau : ça n’aurait pas de sens et l’énoncé stipule que les créneaux impossibles du fichier d’entrée sont cohérents
- l’horaire de début et de fin de créneau ne peuvent pas être égaux (ça n’aurait pas de sens d’avoir un créneau de 0 min !)
- les horaires de début et de fin sont inclus dans la journée de travail donc ils commencent forcément après 07:59 (donc 08:00 min) et avant 18:00 (donc 17:59 max).
Comment trouver les cas particuliers ?
Voici un schéma de tous les cas possibles avec ces contraintes :
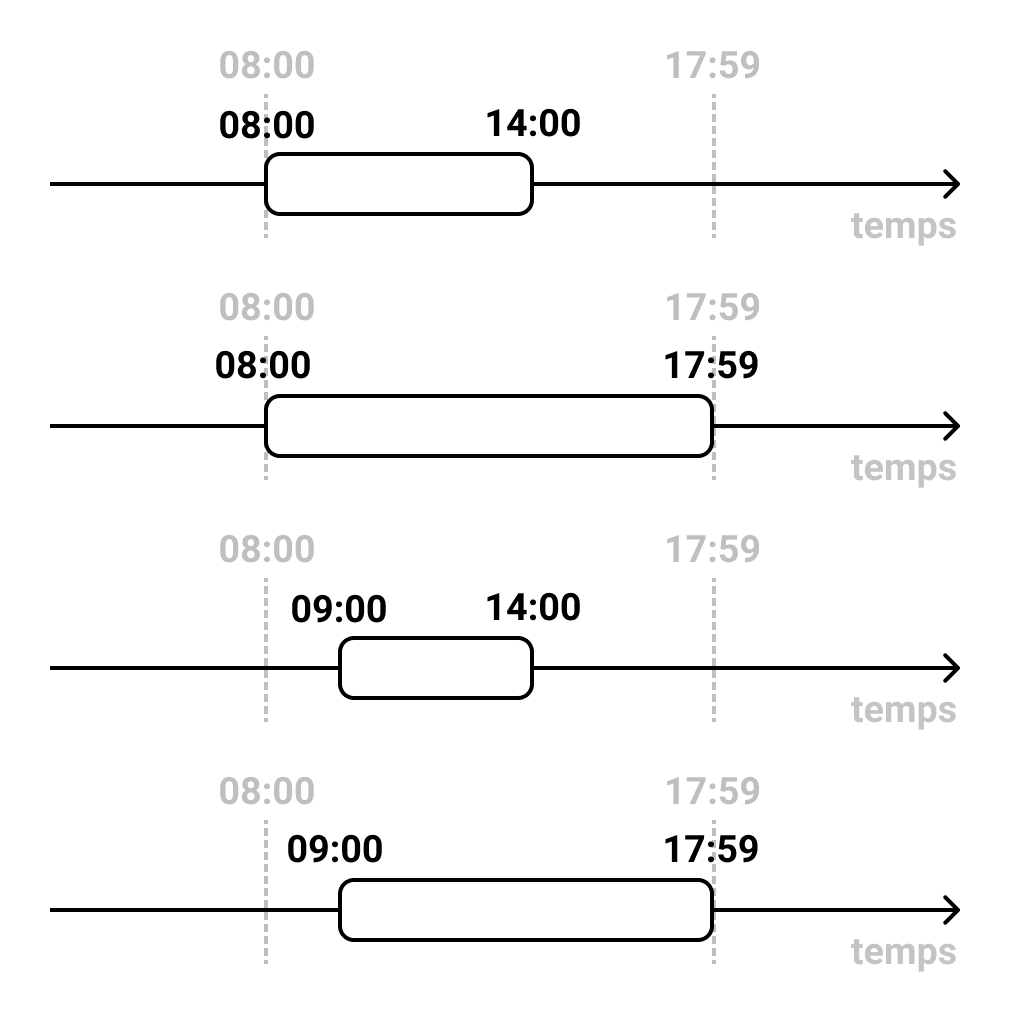
J’ai indiqué des horaires fictifs pour illustrer chaque possibilité :
- 08:00-14:00
- 08:00-17:59
- 09:00-14:00
- 09:00-17:59
Pour trouver ces cas particuliers, il faut procéder par étape en ne faisant varier qu’une seule valeur à la fois.
On ne doit manipuler que 2 valeurs ici : l’horaire de début et l’horaire de fin du créneau. En effet les horaires de début et de fin de journée sont fixes.
Pour trouver toutes les combinaisons possibles, fixons en premier l’horaire de début à une valeur possible puis faisons varier l’horaire de fin.
Quelles sont les valeurs possibles pour l’horaire de début ? Nommons l’horaire de début horaireDebut et le début de journée debutJournee.
On applique la règle des 3 possibilités :
- Soit (
horaireDebut<debutJournee) : l’horaire de début est avant le début de la journée, c’est interdit par l’énoncé car les horaires impossibles sont inclus dans les horaires de journée. On n’a donc pas besoin de tester ce cas. - Soit (
horaireDebut=debutJournee) : l’horaire de début est pile au même moment que le début de la journée soit,horaireDebut= 08:00. - Soit (
horaireDebut>debutJournee) : l’horaire de début est après le début de journée, utilisons une valeur fictive d’exemple dehoraireDebut= 09:00.
Fixons horaireDebut = debutJournee (donc horaireDebut = 08:00), on fait maintenant varier la valeur de l’horaire de fin.
Appelons l’horaire de fin horaireFin et la fin de journée finJournee.
On applique la règle des 3 possibilités :
- Soit (
horaireFin<finJournee) : l’horaire de fin est avant la fin de la journée, prenons comme valeur fictivehoraireFin= 14:00. - Soit (
horaireFin=finJournee) : l’horaire de fin est pile au même moment que la fin de la journée, soithoraireFin= 17:59. - Soit (
horaireFin>finJournee) : l’horaire de fin est après la fin de journée, c’est interdit par l’énoncé car les horaires impossibles sont inclus dans les horaires de journée. On n’a donc pas besoin de tester ce cas.
On a donc 2 combinaisons possibles avec horaireDebut déjà fixé :
horaireDebut= 08:00 ethoraireFin= 14:00horaireDebut= 08:00 ethoraireFin= 17:59
On fait le même travail avec la seconde valeur possible de horaireDebut qu’on fixe maintenant à horaireDebut = 09:00. On obtient 2 combinaisons supplémentaires :
horaireDebut= 09:00 ethoraireFin= 14:00horaireDebut= 09:00 ethoraireFin= 17:59
Ce sont les 4 combinaisons possibles représentées sur le schéma, je vous le remets ici :

Notez que l’énoncé permet de supprimer énormément de combinaisons possibles en interdisant la majorité de celles-ci.
En effet, lorsqu’on compare l’horaire de début et de fin du créneau à l’horaire de début de journée et de fin de journée… il existe en théorie 81 combinaisons possibles ! En effet on fait 4 comparaisons qui peuvent prendre 3 possibilités différentes (soit >, = ou <), ce qui donne 34 combinaisons, soit 81 possibilités.
Je vous les ai notées dans ce tableau (que vous pouvez télécharger en PDF) :
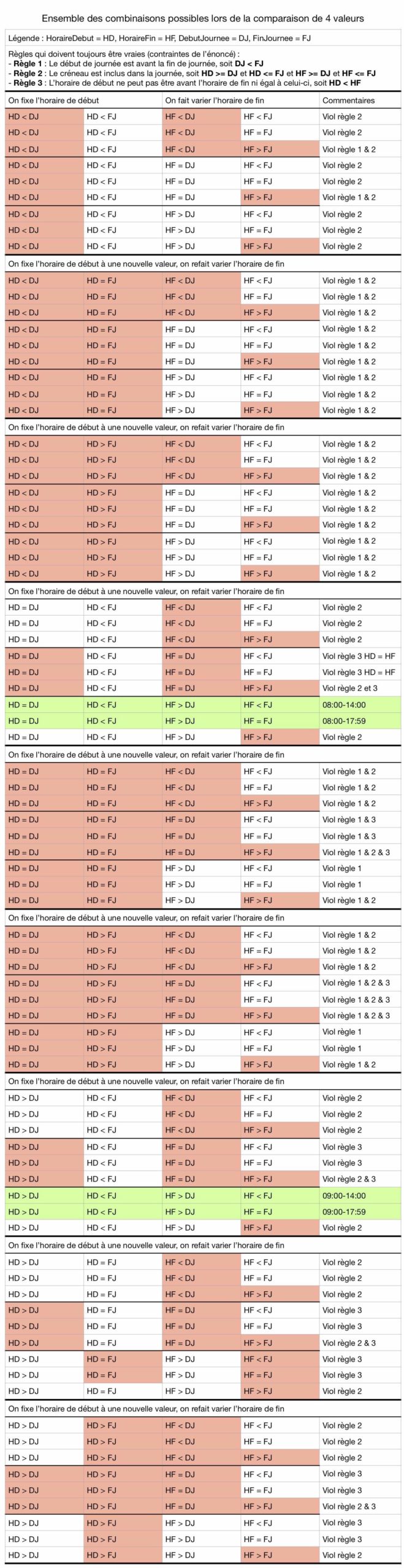
On connaît maintenant tous les cas particuliers à tester sur notre algorithme.
Faites l’essai à la main pour voir si celui-ci fonctionne bien dans tous les cas qu’on a listés. Je vous rappelle l’algorithme ci-dessous et la liste des cas à traiter juste après.
ALGORITHME detecterCreneauDisponible-v0
VARIABLES
CHAINE: debutJournee, finJournee, horaireDebut, horaireFin
DEBUT
debutJournee ← "07:59"
finJournee ← "18:00"
horaireDebut ← lireHoraireDebutDuPremierHoraire()
horaireFin ← lireHoraireFinDuPremierHoraire()
// Est-ce qu'il y a un trou d'au moins 60 minutes entre
// le début de journée et le début du premier horaire ?
SI (dureeTrou(debutJournee, horaireDebut) >= 60) ALORS
afficherReponse(debutJournee)
finDuProgramme
FIN SI
// Est-ce qu'il y a un trou d'au moins 60 minutes entre
// la fin du premier horaire et la fin de la journée ?
SI (dureeTrou(horaireFin, finJournee) >= 60) ALORS
afficherReponse(horaireFin)
finDuProgramme
FIN SI
FIN
Il faut utiliser les valeurs des 4 cas particuliers listés précédemment et vérifier que l’algorithme renvoie la bonne valeur :
- Cas 1 :
horaireDebut= 08:00,horaireFin= 14:00 - Cas 2 :
horaireDebut= 08:00,horaireFin= 17:59 - Cas 3 :
horaireDebut= 09:00,horaireFin= 14:00 - Cas 4 :
horaireDebut= 09:00,horaireFin= 17:59
Notez qu’on est censé toujours avoir un créneau possible garanti d’après l’énoncé, je rappelle la consigne :
Il est garanti qu’il existe au moins une solution. S’il en existe plusieurs, vous pouvez donner n’importe quel horaire valide.
Donc, il aurait fallu supprimer également le cas n°2 de ces cas particuliers, puisqu’il n’existe pas de créneau disponible pour ces valeurs. En effet, le créneau impossible dure toute la journée !
Mais pour expliquer dans la globalité la démarche effectuée pour trouver ces cas particuliers, je le laisse dans la liste. Notez que pour ce cas, l’algorithme n’affichera rien, ce qui n’est pas gênant.
Après vérification de tous les autres cas, on peut voir que notre algorithme traite les cas particuliers avec succès. Ouf ! On peut passer à la suite !
Si on avait eu des erreurs de logique, il aurait fallu prendre en compte le cas particulier posant problème et modifier notre algorithme pour que ça fonctionne à nouveau avec tous les cas possibles : c’est ce qu’on appelle faire une itération.
Ne rentrez pas trop dans les détails
Essayons maintenant de rédiger le code des fonctions qu’on a utilisées dans cet algorithme. Commençons par lireHoraireDebutDuPremierHoraire().
Dans ce concours de programmation, on doit rédiger notre code dans un éditeur en ligne. On nous donne une variable input en entrée que l’on doit lire pour récupérer les données du fichier d’entrée.
Cette variable input est un tableau (une liste de valeurs) qui contient déjà chaque ligne du fichier d’entrée sous la forme d’une chaîne de caractères.
Donc chaque case du tableau correspond à une ligne de l’entrée.
Reprenons notre fichier d’entrée d’exemple :
1 // → input[0] 08:30-09:52 // → input[1]
Dans un tableau on compte à partir de 0, pas de 1.
Donc la 1ère case du tableau, la case de position 0, aussi appelée d’indice 0 contient le nombre de créneaux à lire, soit la valeur « 1 ». On accède à cette case en utilisant la notation input[0]. Soit input[<indice>]. On accède à la case du tableau input d’indice <indice>.
La seconde case du tableau contient le premier créneau à lire « 08:30-09:52 », on y accède avec la notation input[1].
Pour lire l’horaire de début du premier horaire il va donc falloir découper la chaîne « 08:30-09:52 » en deux en utilisant le tiret « – » comme délimiteur de découpage puis récupérer la partie de gauche « 08h30 ».
Comme les horaires ont tous un formatage identique HH:MM-HH:MM, on pourrait également choisir de récupérer les 5 premiers caractères pour l’horaire de début.
On va néanmoins utiliser le découpage avec le tiret qui est plus simple :
ALGORITHME lireHoraireDebutDuPremierHoraire
PARAMETRES globaux
CHAINE: input[]
VARIABLES
CHAINE: tableauChaineDecoupee[]
DEBUT
// On découpe la seconde ligne (case n°1) avec le tiret
tableauChaineDecoupee ← decouper(input[1], '-')
// On récupère la partie de gauche, soit la 1ère case du
// tableau renvoyé
RETOURNER tableauChaineDecoupee[0]
FIN
Alors j’ai utilisé une fonction decouper qui renvoie un tableau de chaînes de caractères qui contient les différentes parties découpées sans le tiret. Vous vous demandez sûrement d’où ça sort ? Comment je sais que je peux utiliser ça dans mon algorithme ?
En vérité, je n’ai pas le droit de l’utiliser !
Je m’inspire ici de la méthode split en JavaScript pour rédiger mon algorithme.
Or lorsqu’on écrit un algorithme, il faut que le pseudo-code reste indépendant du langage de programmation qu’on utilisera pour l’implémenter.
Donc décrire l’algorithme à un niveau si bas (proche des données) est une erreur !
Plus vous vous rapprochez des données à manipuler et plus vous allez devoir utiliser à un moment ou à un autre des possibilités offertes par le langage que vous utiliserez pour implémenter cet algorithme.
Vous ne devez donc pas rentrer dans les détails de votre algorithme.
Vous devez rester au niveau de l’utilisation de lireHoraireDebutDuPremierHoraire et lireHoraireFinDuPremierHoraire.
Vous n’avez pas besoin de décrire l’algorithme de ces fonctions là. Leur code fera partie des détails d’implémentation et on ne peut pas le décrire indépendamment d’un langage de programmation.
Je voulais vous montrer ce problème car vous allez sûrement vous demander à un moment donné : à quel niveau de détails dois-je rédiger mon algorithme ?
La réponse est au plus proche des données sans jamais avoir à rentrer dans les détails d’implémentation qui seront liés au langage de programmation utilisé pour implémenter cet algorithme.
Les fonctions lireHoraireDebutDuPremierHoraire et les autres ont un nom suffisamment explicite pour que le développeur qui devra implémenter cet algorithme sache comment le faire avec son langage de programmation favori.
À la rigueur, vous pouvez ajouter un commentaire dans l’algorithme avec une description de ce que fait la fonction, ce qu’elle devra renvoyer comme type de données (une chaîne de caractères ici) accompagné d’un exemple. Ce sera au développeur de faire l’implémentation finale.
La seule fonction qu’on peut rédiger en gardant un niveau d’abstraction suffisamment élevé et en restant indépendant du langage de programmation c’est afficherReponse(horaire) :
ALGORITHME afficherReponse(horaire)
PARAMETRES locaux
CHAINE: horaire
VARIABLES
ENTIER: heures, minutes, horaireDebutMin, horaireFinMin
CHAINE: horaireDebut, horaireFin
DEBUT
// Ex.: horaire vaut "09:52"
heures ← extraireHeures(horaire)
minutes ← extraireMinutes(horaire)
// Astuce : on transforme tout en minutes pour faire les
// calculs sur les horaires
horaireDebutMin ← heures * 60 + minutes
// On veut obtenir "09:53" car "09:52" fait partie du
// créneau impossible
horaireDebutMin ← horaireDebutMin + 1
// On calcule l'horaire de fin, on veut "10:52"
horaireFinMin ← horaireDebutMin + 59
// Il faudra reconvertir tout ça au format HH:MM
horaireDebut ← convertirMinEnHoraire(horaireDebutMin)
horaireFin ← convertirMinEnHoraire(horaireFinMin)
// On affiche le résultat avec le bon format "09:53-
// 10:52" grâce à une concaténation
AFFICHER(horaireDebut + '-' + horaireFin)
FIN
Vous pouvez télécharger l’algorithme et une implémentation possible de celui-ci en JavaScript (fichiers afficherReponse.algo et afficherReponse.js).
Une fois de plus j’ai utilisé une fonction convertirMinEnHoraire dont le but sera de convertir par exemple 593 minutes sous la forme d’une chaîne de caractères au format HH:MM comme « 09:53 ».
J’ai également utilisé la concaténation pour AFFICHER(horaireDebut + '-' + horaireFin) qui est un concept suffisamment général en programmation pour pouvoir l’exploiter dans un algorithme en restant indépendant de tout langage de programmation.
Ce qui est important ici ce sont les calculs permettant de trouver les bons horaires de début et de fin pour le résultat.
On n’écrira donc pas l’algorithme de convertirMinEnHoraire car sa description serait trop proche du langage utilisé pour l’implémenter (mais vous pouvez voir son implémentation JavaScript dans le fichier ZIP).
Récapitulons !
Nous sommes maintenant capable de trouver un créneau de 60 minutes lorsqu’on a une seule contrainte horaire pour un seul jour donné et ce, même pour les cas particuliers.
Phase 3 : augmentez la difficulté
On va maintenant ajouter un second horaire impossible qu’il va falloir gérer. Voici le nouveau fichier d’entrée d’exemple :
2 08:30-09:52 10:45-14:47
On commence avec un nouvel horaire non superposé et déjà classé dans l’ordre chronologique. Comment faire pour adapter notre algorithme initial detecterCreneauDisponible-v0 à ce nouveau cas de figure ?
Regardons déjà si celui-ci fonctionne pour ce nouvel exemple (on sait jamais), je vous le remets ci-dessous :
ALGORITHME detecterCreneauDisponible-v0
VARIABLES
CHAINE: debutJournee, finJournee, horaireDebut, horaireFin
DEBUT
debutJournee ← "07:59"
finJournee ← "18:00"
horaireDebut ← lireHoraireDebutDuPremierHoraire()
horaireFin ← lireHoraireFinDuPremierHoraire()
// Est-ce qu'il y a un trou d'au moins 60 minutes entre
// le début de journée et le début du premier horaire ?
SI (dureeTrou(debutJournee, horaireDebut) >= 60) ALORS
afficherReponse(debutJournee)
finDuProgramme
FIN SI
// Est-ce qu'il y a un trou d'au moins 60 minutes entre
// la fin du premier horaire et la fin de la journée ?
SI (dureeTrou(horaireFin, finJournee) >= 60) ALORS
afficherReponse(horaireFin)
finDuProgramme
FIN SI
FIN
Le problème de notre algorithme initial, c’est qu’il ne lit que le premier horaire, il faudrait qu’il lise au moins le deuxième horaire. Essayons d’écrire un nouvel algorithme detecterCreneauDisponible-v1 faisant ça.
J’ai déclaré 2 nouvelles variables horaireDebut2 et horaireFin2 qui sont l’horaire de début et de fin du 2ème créneau impossible « 10:45-14:47 ».
J’ai renommé les variables horaireDebut et horaireFin en horaireDebut1 et horaireFin1 pour rester cohérent dans le nom des variables et faciliter la compréhension par la suite lorsqu’on va utiliser une boucle.
J’ai mis en gras les modifications par rapport à la version initiale de l’algorithme.
ALGORITHME detecterCreneauDisponible-v1
VARIABLES
CHAINE: debutJournee, finJournee, horaireDebut1, horaireFin1, horaireDebut2, horaireFin2
DEBUT
debutJournee ← "07:59"
finJournee ← "18:00"
horaireDebut1 ← lireHoraireDebutDuPremierHoraire()
horaireFin1 ← lireHoraireFinDuPremierHoraire()
// Est-ce qu'il y a un trou d'au moins 60 minutes entre
// le début de journée et le début du premier horaire ?
SI (dureeTrou(debutJournee, horaireDebut1) >= 60) ALORS
afficherReponse(debutJournee)
finDuProgramme
FIN SI
horaireDebut2 ← lireHoraireDebutDuDeuxiemeHoraire()
horaireFin2 ← lireHoraireFinDuDeuxiemeHoraire()
// Est-ce qu'il y a un trou d'au moins 60 minutes entre
// la fin du premier horaire et le début du 2ème horaire ?
SI (dureeTrou(horaireFin1, horaireDebut2) >= 60) ALORS
afficherReponse(horaireFin1)
finDuProgramme
FIN SI
// Est-ce qu'il y a un trou d'au moins 60 minutes entre
// la fin du 2ème horaire et la fin de journée ?
SI (dureeTrou(horaireFin2, finJournee) >= 60) ALORS
afficherReponse(horaireFin2)
finDuProgramme
FIN SI
FIN
Il a fallu ajouter une étape supplémentaire de vérification d’existence d’un trou de 60 minutes entre les 2 horaires, c’est-à-dire entre la fin du 1er horaire et le début du 2ème horaire.
Lorsqu’on fait une itération sur un algorithme, c’est-à-dire qu’on l’améliore pour répondre à un nouveau besoin (ici gérer 2 créneaux impossibles au lieu d’1), il faut vérifier qu’il réponde toujours au besoin auquel il répondait précédemment !
Est-ce que ce nouvel algorithme peut gérer notre fichier d’exemple précédent qui ne possédait qu’un seul créneau impossible ?
La réponse est non ! On a un problème.
Il va falloir remanier le code pour qu’il puisse gérer le cas avec un seul horaire plus ce nouveau cas avec 2 horaires.
Pour ça il va falloir utiliser une boucle qui va permettre de s’adapter au nombre de créneaux qu’on trouvera dans le fichier d’entrée. On va profiter de ce remaniement pour factoriser aussi le code qui se répète beaucoup.
On l’avait déjà vu, ce code se répète plusieurs fois :
SI (dureeTrou(debut, fin) >= 60) ALORS
afficherReponse(debut)
finDuProgramme
FIN SI
Et on a également celui-ci qui se répète et qui est très similaire :
horaireDebut1 ← lireHoraireDebutDuPremierHoraire() horaireFin1 ← lireHoraireFinDuPremierHoraire() horaireDebut2 ← lireHoraireDebutDuDeuxiemeHoraire() horaireFin2 ← lireHoraireFinDuDeuxiemeHoraire()
Il va donc falloir trouver un moyen d’intégrer ces 2 portions de code dans notre boucle pour factoriser tout ça !
Par ailleurs, par souci de simplicité on a dupliqué des fonctions fortement similaires.
En effet, les fonctions lireHoraireDebutDuPremierHoraire et lireHoraireDebutDuDeuxiemeHoraire sont très similaires donc on peut les fusionner (pareil pour lireHoraireFinDuPremierHoraire et lireHoraireFinDuDeuxiemeHoraire).
Comment faire cette fusion ? En créant seulement 2 fonctions prenant un paramètre qui serait la position de l’horaire à lire.
Par exemple une fonction lireHoraireDebutDeCreneau(1) permettrait de lire l’horaire de début du 1er créneau et une fonction lireHoraireFinDeCreneau(1) permettrait de lire l’horaire de fin du 1er créneau.
On pourrait alors réécrire notre code comme ceci :
horaireDebut1 ← lireHoraireDebutDeCreneau(1) horaireFin1 ← lireHoraireFinDeCreneau(1) horaireDebut2 ← lireHoraireDebutDeCreneau(2) horaireFin2 ← lireHoraireFinDeCreneau(2)
Au lieu d’avoir 4 fonctions on n’en a plus que 2.
De plus, utiliser un paramètre dans ces fonctions va nous permettre de les utiliser facilement dans notre boucle comme on va le voir juste après.
Construction d’une boucle adéquate
Pour construire notre boucle, il va falloir s’intéresser au code qui se répète dans notre algorithme et donc aux tests qu’on effectuent. Lorsqu’on travaille avec un seul créneau, voici dans l’ordre les tests à effectuer :
SI (dureeTrou(debutJournee, horaireDebut1) >= 60) SI (dureeTrou(horaireFin1, finJournee) >= 60)
Lorsqu’on a 2 créneaux impossibles, voici dans l’ordre les tests à effectuer :
SI (dureeTrou(debutJournee, horaireDebut1) >= 60) SI (dureeTrou(horaireFin1, horaireDebut2) >= 60) SI (dureeTrou(horaireFin2, finJournee) >= 60)
On voit qu’ils sont très similaires, ce qui est plutôt bon signe pour factoriser ce code sous la forme d’une boucle ! Et on peut se rendre compte de la logique à appliquer pour tester entre eux les différents horaires.
Poussons encore un peu plus loin la réflexion avec un exemple fictif de 3 créneaux impossibles, voici ce que ça donnerait :
SI (dureeTrou(debutJournee, horaireDebut1) >= 60) SI (dureeTrou(horaireFin1, horaireDebut2) >= 60) SI (dureeTrou(horaireFin2, horaireDebut3) >= 60) SI (dureeTrou(horaireFin3, finJournee) >= 60)
Et voici une représentation visuelle des comparaisons à effectuer pour le cas où il y a 3 créneaux :
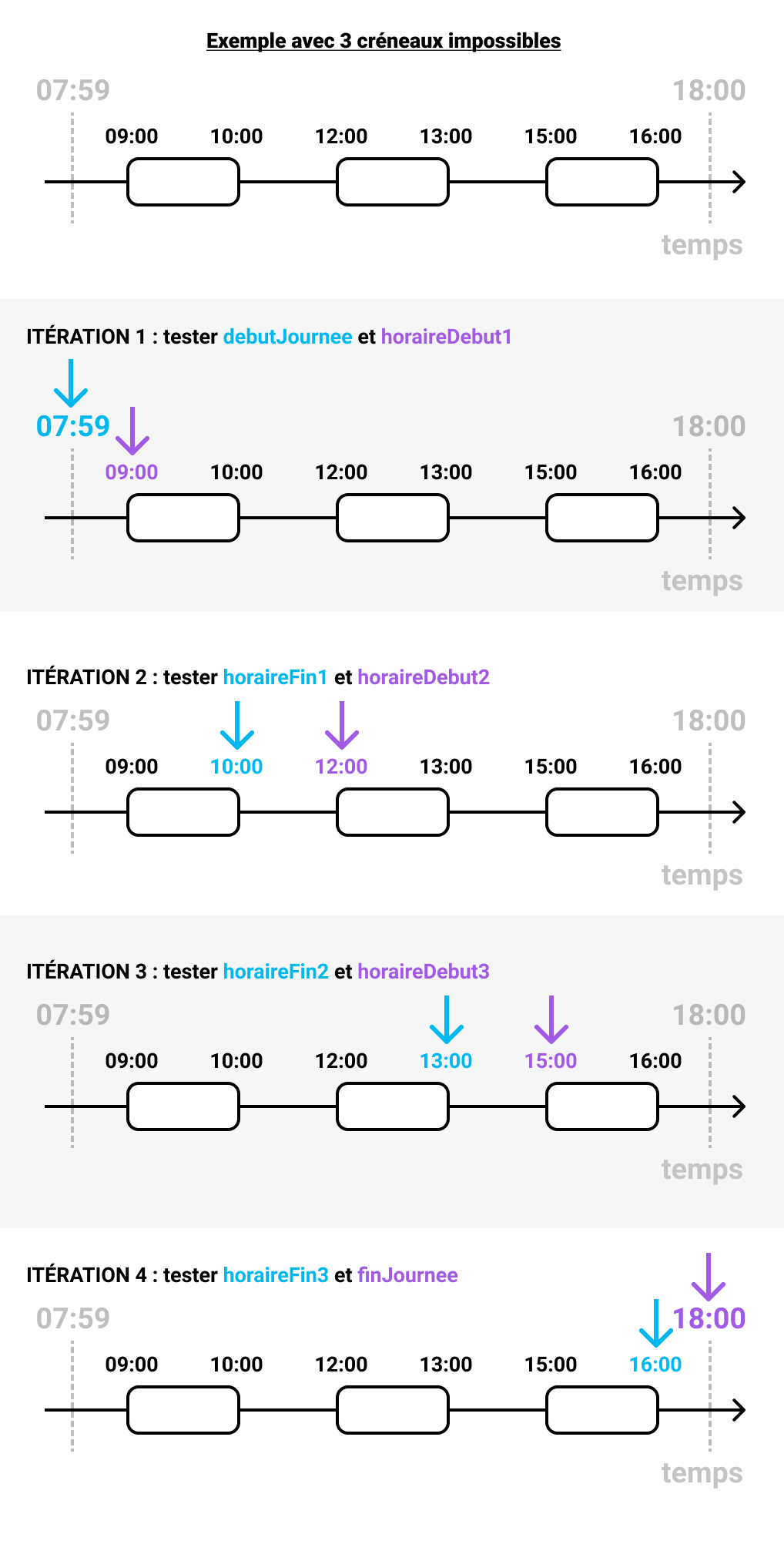
On voit ici qu’on aura besoin de faire 4 itérations pour 3 créneaux impossibles, on peut en déduire qu’il faudra donc N+1 itérations pour N créneaux impossibles.
On peut vérifier cette formule : pour 1 créneau on a vu qu’il fallait 2 tests, pour 2 créneaux il faut 3 tests, pour 3 créneaux il faut 4 tests, ça correspond bien à notre formule : pour N créneaux il faut N+1 tests.
On voit aussi qu’on compare toujours 2 à 2 les créneaux de la même façon : les flèches bleues et violettes se « déplacent » vers la droite en restant toujours côte à côte. On va donc pouvoir utiliser une boucle pour tester ces valeurs.
Le code de test à l’intérieur de la boucle sera :
SI (dureeTrou(debut, fin) >= 60) ALORS
afficherReponse(debut)
finDuProgramme
FIN SI
Et on fera varier les valeurs de debut et fin au fur et à mesure qu’on progresse dans la boucle et qu’on compare les créneaux entre eux.
Par exemple, pour 3 créneaux les variables debut et fin prendront les valeurs suivantes :
- Itération 1 :
debut=debutJourneeetfin=horaireDebut1 - Itération 2 :
debut=horaireFin1etfin=horaireDebut2 - Itération 3 :
debut=horaireFin2etfin=horaireDebut3 - Itération 4 :
debut=horaireFin3etfin=finJournee
Maintenant il faut attaquer la partie difficile et rédiger l’algorithme ! Appelons celui-ci detecterCreneauDisponible-v2
Voici une proposition possible pour cet algorithme (explications après l’algorithme) :
ALGORITHME detecterCreneauDisponible-v2
// La variable input contient déjà les données d'entrée
// C'est un tableau dont chaque case contient une ligne du fichier d'entrée
VARIABLES globales
CHAINE: input[] // tableau de chaînes de caractères
VARIABLES
CHAINE: debutJournee, finJournee, debut, fin
ENTIER: nombreCreneaux, nombreDeTestsAFaire, position
DEBUT
debutJournee ← "07:59"
finJournee ← "18:00"
// Sur la première ligne du fichier d'entrée on lit le nombre de créneaux
nombreCreneaux ← input[0]
// Il faut N+1 tests
nombreDeTestsAFaire ← nombreCreneaux + 1
// On connaît le nombre de tests à effectuer
POUR position ALLANT DE 1 À nombreDeTestsAFaire PAR PAS DE 1 FAIRE
// Pour le 1er test on utilise debutJournee
SI (position = 1) ALORS
debut ← debutJournee
SINON
// Lors du test 2 il faut prendre la fin du créneau 1
debut ← lireHoraireFinDeCreneau(position - 1)
FIN SI
// Pour le dernier test, il faut utiliser finJournee !
SI (position = nombreDeTestsAFaire) ALORS
fin ← finJournee
SINON
fin ← lireHoraireDebutDeCreneau(position)
FIN SI
SI (dureeTrou(debut, fin) >= 60) ALORS
afficherReponse(debut)
finDuProgramme
FIN SI
FIN POUR
FIN
Vous pouvez télécharger l’algorithme et une implémentation possible de celui-ci en JavaScript (fichiers detecterCreneauDisponibleV2.algo et detecterCreneauDisponibleV2.js).
On aurait pu écrire cet algorithme de plein de façons différentes, j’ai choisi ici une façon simple qui s’adresse aux débutants et qui est facile à comprendre suite à tout ce qui a déjà été dit dans cet article.
J’ai utilisé une variable position pour savoir où on en est dans les tests à effectuer. Cette variable prend les valeurs de 1 à N+1. Donc pour 3 créneaux, elle prend les valeurs 1, 2, 3 puis 4.
Grâce à cette variable on peut aisément sélectionner le bon créneau pour pouvoir récupérer soit l’horaire de début soit l’horaire de fin qui nous intéresse et mettre ainsi à jour les variables debut et fin utilisées dans le test à l’intérieur de la boucle.
Dernière étape il faut vérifier que ce code fonctionne avec un seul créneau (avec les 4 cas particuliers lorsqu’on a un créneau). On peut le vérifier à la main, c’est bien le cas !
On est donc maintenant capable de gérer plusieurs créneaux impossibles. On peut passer à la suite.
Il reste encore 2 parties complexes à gérer : la superposition des créneaux et leur possible désordre chronologique !
Attaquons la partie la plus simple : le désordre chronologique.
Trier dans l’ordre chronologique les créneaux
Reprenons notre fichier d’entrée d’exemple précédent :
2
08:30-09:52
10:45-14:47
Celui-ci est trié dans l’ordre chronologique mais que se passe-t-il si on le met dans le désordre ? Par exemple :
2 10:45-14:47 08:30-09:52
Est-ce que notre algorithme detecterCreneauDisponible-v2 fonctionne toujours ? Eh bien non !
En effet si on utilise notre algorithme sur ce fichier d’exemple, il va trouver un créneau possible de 60 min dès la 1ère comparaison entre le début de la journée à 07:59 et l’horaire de début du 1er créneau à 10:45.
Évidemment, ce n’est pas la bonne réponse… Il va donc falloir trier dans l’ordre nos données d’entrée avant de passer notre tableau de créneaux à cet algorithme.
Pour trier cette liste de créneaux, il va falloir se baser sur l’horaire de début des créneaux uniquement. Pour cet exemple, il faut lire 10:45 et 08:30 et décider lequel vient en 1er, c’est 08:30 bien sûr !
C’est facile en tant qu’être humain de savoir la réponse, mais quelles sont les étapes à faire pour comparer ces horaires ? Il faut les décrire pour l’ordinateur.
En tant qu’être humain, comment faites-vous pour comparer 2 horaires entre eux ? Une façon de faire c’est de :
- Comparer le nombre d’heures (ici 10 et 08) : s’il est différent, alors l’horaire qui a le plus petit nombre d’heures sera placé avant l’autre dans la liste.
- Si le nombre d’heures est identique, on compare le nombre de minutes : celui qui a la plus petite valeur viendra avant l’autre dans la liste.
C’est une façon très classique de faire et parfaitement viable.
On peut également partir sur des solutions alternatives comme convertir les horaires en minutes et comparer les valeurs entre elles. Par exemple, 10:45 devient 10 * 60 + 45 = 645 min et 08:30 devient 8 * 60 + 30 = 510 min. On compare 645 et 510 : 510 est inférieur donc 08:30 vient avant 10:45.
On peut aussi utiliser l’ordre lexicographique (c’est une notion avancée, ce n’est pas grave si vous ne comprenez pas) et faire un tri direct entre la chaîne de caractères « 10:45 » et « 08:30 ». Grâce au format HH:MM on va comparer un à un les caractères de chaque horaire pour déterminer lequel vient avant l’autre.
Dès qu’un caractère vient avant l’autre alors cet horaire vient avant l’autre. Si les caractères qu’on comparent sont identiques on passe au caractère suivant.
Pour notre exemple on compare le 1er caractère « 1 » (de « 10:45 ») et « 0 » (de « 08:30 »). « 0 » vient avant « 1 » dans la liste des caractères donc 08:30 vient avant 10:45.
Notez que cette approche n’est possible que grâce au format strict HH:MM. Si on comparait « 10:45 » avec « 8:30 » (au lieu de « 08:30 »), à la première comparaison on comparerait le « 1 » de « 10:45 » avec le « 8 » de « 8:30 » et on tirerait la conclusion fausse que 10:45 vient avant 8:30 !
On pourrait également utiliser le type Date en JavaScript pour gérer les horaires… bref, il y a plein de solutions.
Alors on pourrait rédiger un algorithme pour trier un tableau complet de créneaux mais c’est un exercice pas tellement drôle à faire et surtout les langages de programmation sont déjà tous équipés de méthodes de tri permettant de faire ça facilement.
Par exemple en JavaScript on a la méthode sort() qui permet de trier un tableau d’une certaine façon. Cette méthode prend en paramètre une fonction qui va comparer 2 à 2 chaque case du tableau et le trier. Nommons les 2 cases comparées case1 et case2.
La fonction qu’on passe à sort() doit renvoyer une valeur numérique qui déterminera l’ordre de tri des éléments du tableau :
- Si la fonction renvoie une valeur inférieure à 0 alors on placera
case1avantcase2. - Si la fonction renvoie la valeur 0 alors on ne changera pas l’ordre de
case1etcase2dans le tableau. - Si la fonction renvoie une valeur supérieure à 1 alors on placera
case1aprèscase2.
Vous vous souvenez que notre algorithme doit être indépendant du langage de programmation. Donc en théorie, notre étape préalable de tri du tableau devrait s’écrire :
nombreCreneaux ← input[0] // On ne récupère que la liste des créneaux, soit les cases // 1 à N (nombre de créneaux) du tableau input creneaux ← input[1..nombreCreneaux] // On trie dans l'ordre chronologique creneaux ← trierParOrdreChronologique(creneaux)
Et on pourrait expliquer au développeur chargé d’implémenter cet algorithme comment la fonction trierParOrdreChronologique doit se comporter, le reste est du détail d’implémentation lié au langage de programmation.
Mais pour cet article on va écrire l’algorithme de la fonction qu’on va passer à sort() à titre d’exercice. On va utiliser l’approche « naturelle » de comparer les heures et les minutes :
FONCTION fonctionDeTriChronologique(creneau1, creneau2)
PARAMETRES locaux
CHAINE: creneau1, creneau2
DEBUT
// creneau1 vaut par exemple "10:45-14:47"
// creneau2 vaut par exemple "08:30-09:52"
// On récupère juste l'horaire de début des créneaux
horaireDebut1 ← lireHoraireDebutDeCreneau(creneau1)
horaireDebut2 ← lireHoraireDebutDeCreneau(creneau2)
heuresDebut1 ← extraireHeures(horaireDebut1)
heuresDebut2 ← extraireHeures(horaireDebut2)
SI (heuresDebut1 = heuresDebut2) ALORS
// On compare les minutes
minutesDebut1 ← extraireMinutes(horaireDebut1)
minutesDebut2 ← extraireMinutes(horaireDebut2)
// Utiliser une soustraction permet de renvoyer une
// valeur négative, positive ou nulle comme demandé
RETOURNER (minutesDebut1 - minutesDebut2)
FIN SI
// Utiliser une soustraction permet de renvoyer une
// valeur négative, positive ou nulle comme demandé
RETOURNER (heuresDebut1 - heuresDebut2)
FIN
Vous pouvez télécharger l’algorithme et une implémentation possible de celui-ci en JavaScript (fichiers fonctionDeTriChronologique.algo et fonctionDeTriChronologique.js).
Ici on utilise l’astuce de la soustraction (que vous trouverez dans la documentation) pour renvoyer une valeur négative, positive ou nulle en fonction de la comparaison.
On aurait pu également écrire le code suivant, qui est tout à fait juste, mais un peu moins élégant :
SI (minutesDebut1 = minutesDebut2) ALORS RETOURNER 0 FIN SI SI (minutesDebut1 < minutesDebut2) ALORS RETOURNER -1 SINON RETOURNER 1 FIN SI
Notez qu’on a utilisé à nouveau une fonction lireHoraireDebutDeCreneau mais c’est une version un peu différente de la précédente fonction du même nom. En effet, la version précédente utilisait la position de la case du tableau input en tant que paramètre.
Ici on utilise directement comme paramètre une chaîne de caractères qui représente un créneau impossible comme par exemple « 10:45-14:47 ». Il faudra donc adapter un peu le code original comme on va le voir tout de suite.
Je vous remets le code précédent de notre algorithme detecterCreneauDisponible-v2 qui ne gère pas encore le tri par ordre chronologique, c’est la version 2 (v2) :
ALGORITHME detecterCreneauDisponible-v2
// La variable input contient déjà les données d'entrée
// C'est un tableau dont chaque case contient une ligne du fichier d'entrée
VARIABLES globales
CHAINE: input[] // tableau de chaînes de caractères
VARIABLES
CHAINE: debutJournee, finJournee, debut, fin
ENTIER: nombreCreneaux, nombreDeTestsAFaire, position
DEBUT
debutJournee ← "07:59"
finJournee ← "18:00"
// Sur la première ligne du fichier d'entrée on lit le nombre de créneaux
nombreCreneaux ← input[0]
// Il faut N+1 tests
nombreDeTestsAFaire ← nombreCreneaux + 1
// On connaît le nombre de tests à effectuer
POUR position ALLANT DE 1 À nombreDeTestsAFaire PAR PAS DE 1 FAIRE
// Pour le 1er test on utilise debutJournee
SI (position = 1) ALORS
debut ← debutJournee
SINON
// Lors du test 2 il faut prendre la fin du créneau 1
debut ← lireHoraireFinDeCreneau(position - 1)
FIN SI
// Pour le dernier test, il faut utiliser finJournee !
SI (position = nombreDeTestsAFaire) ALORS
fin ← finJournee
SINON
fin ← lireHoraireDebutDeCreneau(position)
FIN SI
SI (dureeTrou(debut, fin) >= 60) ALORS
afficherReponse(debut)
finDuProgramme
FIN SI
FIN POUR
FIN
Et maintenant rédigeons le nouvel algorithme qu’on va appeler detecterCreneauDisponible-v3 (version 3) qui prendra en compte ce travail préalable de tri du tableau des créneaux.
Il prendra également en compte la petite modification apportée à la fonction lireHoraireDebutDeCreneau qui ne prend plus une position en paramètre mais bien directement une chaîne de caractères correspondant à un créneau.
Notez que pour conserver une certaine cohérence on modifiera également sa fonction sœur lireHoraireFinDeCreneau pour qu’elle prenne également un créneau en paramètre et non plus la position dans le tableau input.
Autre point très important à noter : on va travailler non plus sur input mais sur un nouveau tableau creneaux qui contiendra les créneaux triés ! Il faudra donc ajuster la valeur de position dans le code.
En effet, quand on s’intéressait aux créneaux avec input, la 1ère case (d’indice 0) n’était jamais utilisée puisqu’elle contenait le nombre de créneaux à lire et pas un créneau.
Dans le nouveau tableau creneaux qu’on va maintenant utiliser la 1ère case correspondra au 1er créneau : on va donc commencer à compter à partir de 0 dans notre boucle !
J’ai noté en gras les modifications apportées par rapport à la v2 :
ALGORITHME detecterCreneauDisponible-v3
// La variable input contient déjà les données d'entrée
// C'est un tableau dont chaque case contient une ligne du fichier d'entrée
VARIABLES globales
CHAINE: input[] // tableau de chaînes de caractères
VARIABLES
CHAINE: debutJournee, finJournee, debut, fin, creneaux[]
ENTIER: nombreCreneaux, nombreDeTestsAFaire, position
DEBUT
debutJournee ← "07:59"
finJournee ← "18:00"
// Sur la première ligne du fichier d'entrée on lit le nombre de créneaux
nombreCreneaux ← input[0]
// Il faut N+1 tests
nombreDeTestsAFaire ← nombreCreneaux + 1
// On récupère juste les créneaux pour les trier
// Soit les cases 1 à nombreCreneaux du tableau input
creneaux ← input[1..nombreCreneaux]
// On trie par ordre chronologique
creneaux ← trierParOrdreChronologique(creneaux)
// On connaît le nombre de tests à effectuer
POUR position ALLANT DE 0 À nombreDeTestsAFaire - 1 PAR PAS DE 1 FAIRE
// Pour le 1er test on utilise debutJournee
SI (position = 0) ALORS
debut ← debutJournee
SINON
// Lors du test 2 il faut prendre la fin du créneau 1
debut ← lireHoraireFinDeCreneau(creneaux[position - 1])
FIN SI
// Pour le dernier test, il faut utiliser finJournee !
SI (position = nombreDeTestsAFaire - 1) ALORS
fin ← finJournee
SINON
fin ← lireHoraireDebutDeCreneau(creneaux[position])
FIN SI
SI (dureeTrou(debut, fin) >= 60) ALORS
afficherReponse(debut)
finDuProgramme
FIN SI
FIN POUR
FIN
Vous pouvez télécharger l’algorithme et une implémentation possible de celui-ci en JavaScript (fichiers detecterCreneauDisponibleV3.algo et detecterCreneauDisponibleV3.js).
On a ici ajusté la valeur de position dans notre boucle : le 1er test est effectué quand position vaut 0 et le dernier quand position vaut nombreDeTestsAFaire - 1.
Eh oui, pour obtenir 5 tests par exemple on compte 1,2,3,4,5 (on a bien 5 itérations de 1 à nombreDeTestsAFaire) mais si on compte à partir de zéro il faut faire 0,1,2,3,4 (5 itérations de 0 à nombreDeTestsAFaire - 1) !
On utilise aussi maintenant directement le créneau dont on veut extraire l’horaire de début ou de fin et non plus la position de celui-ci dans input en passant en paramètre creneaux[position - 1] et creneaux[position] à nos nouvelles fonctions lireHoraireDebutDeCreneau et lireHoraireFinDeCreneau.
Récapitulons : avec cette v3 on est maintenant capable de gérer plusieurs créneaux impossibles qui peuvent être dans le désordre ! C’est déjà pas mal non ?
Passons au dernier point difficile : la superposition de créneaux.
Filtrer les créneaux superposés
On l’a vu précédemment, les créneaux peuvent se « chevaucher ». Prenons un exemple de fichier d’entrée avec des créneaux superposés :
2 10:45-14:15 08:30-12:00
Comme notre algorithme v3 est maintenant capable de trier les créneaux dans l’ordre chronologique on peut se permettre de ne travailler que sur des exemples dont les créneaux sont triés. Reformulons donc notre exemple trié :
2 08:30-12:00 10:45-14:15
Le 2ème créneau commence à 10:45, soit en plein milieu du 1er créneau ! Est-ce que ça pose problème pour notre algorithme v3 ? Non. En effet voici les tests et conclusions qu’il va effectuer pour cet exemple précis :
- Itération 1 : calcule la durée du trou entre 07:59 et 08:30 = 30 min, on avance
- Itération 2 : calcule la durée du trou entre 12:00 et 10:45 = –76 min (négatif), ce n’est pas >= 60 donc on avance
- Itération 3 : calcule la durée du trou entre 14:15 et 18:00 = 224 min => c’est bon on a un créneau de 60 min possible à partir de 14:16.
Pour cet exemple précis, ça ne pose pas de problèmes.
Mais quelles sont toutes les possibilités de superpositions ? Est-ce qu’il y en a qui vont poser problème ?
Reprenons la règle des 3 possibilités avec les contraintes suivantes en tête :
- Les créneaux sont triés dans l’ordre chronologique donc le début du 2ème créneau est soit identique au début du 1er créneau soit après celui-ci
- La fin d’un créneau est toujours après le début de ce créneau : un créneau doit être cohérent et ne peut pas avoir une durée de 0 min
- On compare 2 créneaux entre eux donc le début de journée et la fin de journée n’ont plus d’importance ici
Avec ces contraintes en tête on peut dessiner visuellement les possibilités de superpositions de 2 créneaux, le 1er en bleu, le 2ème en violet :
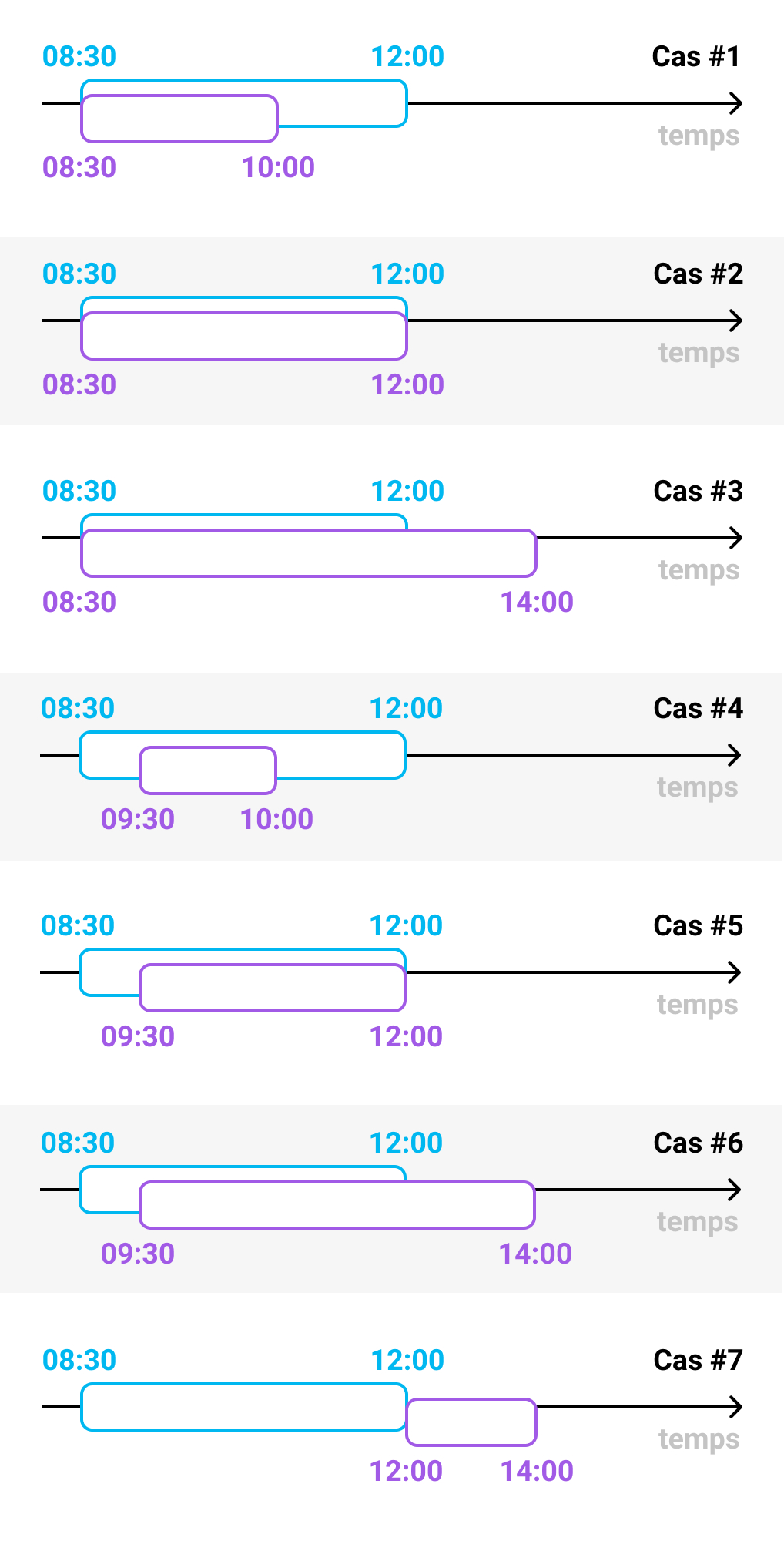
Si on utilise notre algorithme v3 pour les 7 cas possibles de superpositions, on s’aperçoit que ça pose problème pour les cas #1 et #4.
En effet, prenons l’exemple du cas #4 avec :
2 08:30-12:00 09:30-10:00
Pour ce cas particulier, notre algorithme effectuerait les tests suivants :
- Itération 1 : calcule la durée du trou entre 07:59 et 08:30 = 30 min, on avance
- Itération 2 : calcule la durée du trou entre 12:00 et 09:30 = -151 min (négatif), ce n’est pas >= 60 donc on avance
- Itération 3 : calcule la durée du trou entre 10:00 et 18:00 = 479 min => c’est bon on a un créneau de 60 min possible à partir de 10:01, ce qui n’est PAS la bonne réponse !
On obtient une réponse fausse comme quoi un créneau de 60 min est disponible à partir de 10:01 or le 1er créneau indique que c’est impossible de 08:30 à 12:00, ce cas particulier pose donc problème à notre algorithme.
Regardons d’un peu plus près le cas #1 et #4 : qu’ont-ils de commun ? Pourquoi ça pose un problème à notre algorithme ?
Après une rapide analyse on s’aperçoit que l’horaire de fin du 2ème créneau s’arrête toujours avant l’horaire de fin du 1er créneau dans ces 2 cas. C’est là la source de notre problème.
Il faut donc qu’on détecte cette particularité et qu’on agisse. Plusieurs solutions s’offrent à nous :
- On peut supprimer complètement le 2ème créneau de la liste puisque celui-ci est déjà « inclus » dans le 1er créneau (ces bornes sont à l’intérieur du 1er créneau)
- On peut modifier l’horaire de fin de ce 2ème créneau pour le remplacer par l’horaire de fin du 1er créneau et ainsi combler le « trou » qui pose problème pour obtenir la bonne réponse avec notre algorithme
On va partir sur la 1ère solution.
Il va falloir filtrer les créneaux pour retirer ces fameux cas particuliers ou l’horaire de fin du 2ème créneau vient avant l’horaire de fin du 1er créneau.
On va construire à nouveau une boucle qui va comparer 2 à 2 les créneaux préalablement triés par ordre chronologique pour détecter les superpositions.
On stockera les créneaux utiles dans un nouveau tableau creneauxSansSuperpositions qui contiendra tous les créneaux triés dans l’ordre chronologique et ne posant pas le problème des cas #1 et #4.
Pour détecter les superpositions, il nous suffit de regarder si un créneau vient avant un autre ou pas. Et pour ça, on possède déjà une fonction prête à l’emploi !
En effet, la fonction dureeTrou renvoie une valeur négative si les 2 horaires passés en paramètres sont égaux ou si le 1er vient après le second dans le temps.
Exemple 1 : dureeTrou("12:00", "09:30") renvoie -151 min.
Exemple 2 : dureeTrou("12:00", "12:00") renvoie -1 min.
On pourra donc détecter que la fin du créneau 2 vient avant la fin du créneau 1 en testant la valeur renvoyée par dureeTrou(horaireFinCreneau1, horaireFinCreneau2).
Si cette valeur est strictement inférieure à -1, on est dans le cas particulier qu’on cherche à filtrer. Si cette valeur est supérieure ou égale à -1 alors on n’est pas dans le cas particulier (soit les horaires sont égaux soit les horaires sont dans le bon ordre chronologique).
Deuxième point important avant de rédiger l’algorithme : il faudra toujours garder une référence vers l’horaire de fin qu’on utilisera pour faire la comparaison avec le prochain horaire.
En effet si un créneau doit être supprimé de la liste, celui-ci ne devra plus être utilisé pour effectuer une comparaison ! Il faudra utiliser le dernier créneau valide précédent. On appellera ce créneau le créneau de référence, c’est le créneau bleu sur le schéma précédent.
Par extension l’horaire de fin du créneau de référence sera appelé horaireFinReference.
Appelons cet algorithme filtrerSuperpositions, voici une proposition possible et les explications juste après :
FONCTION filtrerSuperpositions(creneaux)
PARAMETRES locaux
CHAINE: creneaux[] // nos créneaux déjà triés
VARIABLES
CHAINE: creneauxSansSuperpositions[] // le futur résultat
ENTIER: position
DEBUT
// On récupère le nombre de créneaux à filtrer
nombreCreneaux ← tailleDuTableau(creneaux)
// Le 1er créneau est forcément bon, on l'ajoute donc à notre liste
ajouterDansTableau(creneauxSansSuperpositions, creneaux[0])
// On initialise l'horaire de fin de référence à celui du 1er créneau
horaireFinReference ← lireHoraireFinDeCreneau(creneaux[0])
// On commence la boucle à partir de 1 car on veut comparer le 2ème
// créneau avec le 1er
POUR position ALLANT DE 1 À nombreCreneaux - 1 PAR PAS DE 1 FAIRE
horaireFin ← lireHoraireFinDeCreneau(creneaux[position])
// Si on n'est PAS dans le cas particulier
SI dureeTrou(horaireFinReference, horaireFin) >= -1 ALORS
// On ajoute ce créneau à notre nouvelle liste
ajouterDansTableau(creneauxSansSuperpositions, creneaux[position])
// On utilise ce créneau valide comme nouvelle
// référence pour la prochaine comparaison
horaireFinReference ← lireHoraireFinDeCreneau(creneaux[position])
FIN SI
FIN POUR
// On retourne tous les créneaux valides filtrés
RETOURNER creneauxSansSuperpositions
FIN
Vous pouvez télécharger l’algorithme et une implémentation possible de celui-ci en JavaScript (fichiers filtrerSuperpositions.algo et filtrerSuperpositions.js).
Dans cet algorithme, j’ai utilisé une fonction tailleDuTableau(tableau) pour récupérer la taille (aussi appelée longueur) d’un tableau passé en paramètre. C’est une fonctionnalité présente dans tous les langages de programmation donc on peut l’indiquer dans un algorithme en pseudo-code.
J’ai également utilisé une fonction ajouterDansTableau(tableau, nouvelElement) qui permet d’ajouter un nouvel élément à la fin d’un tableau. À nouveau c’est une fonctionnalité commune à tous les langages de programmation.
On aurait pu également écrire à la place (on compte à partir de zéro) :creneauxSansSuperpositions[position - 1] ← creneaux[position].
Au final, lorsqu’on tombe sur le cas particulier le code de notre algorithme ne semble rien faire : il n’y a pas d’instructions de suppression du créneau.
C’est normal, puisqu’on on construit à partir de zéro un nouveau tableau qui ne contient que les créneaux utiles pour nous. Donc lorsqu’on détecte un créneau inutile, on ne l’ajoute tout simplement pas à creneauxSansSuperpositions.
C’est pour ça qu’on teste si on est dans le cas normal au lieu de tester si on est dans le cas particulier dans notre algorithme.
Il reste à intégrer cette nouvelle fonctionnalité dans notre algorithme principal qu’on va passer en version 4 !
Le point critique ici c’est que ce filtrage peut modifier la taille du tableau initial contenant les créneaux (si on en supprime), il va donc falloir calculer le nombre de tests à effectuer après avoir filtré les créneaux.
Comme d’habitude je vous remets l’ancien algorithme v3 ici puis la v4 juste après.
ALGORITHME detecterCreneauDisponible-v3
// La variable input contient déjà les données d'entrée
// C'est un tableau dont chaque case contient une ligne du fichier d'entrée
VARIABLES globales
CHAINE: input[] // tableau de chaînes de caractères
VARIABLES
CHAINE: debutJournee, finJournee, debut, fin, creneaux[]
ENTIER: nombreCreneaux, nombreDeTestsAFaire, position
DEBUT
debutJournee ← "07:59"
finJournee ← "18:00"
// Sur la première ligne du fichier d'entrée on lit le nombre de créneaux
nombreCreneaux ← input[0]
// Il faut N+1 tests
nombreDeTestsAFaire ← nombreCreneaux + 1
// On récupère juste les créneaux pour les trier
// Soit les cases 1 à nombreCreneaux du tableau input
creneaux ← input[1..nombreCreneaux]
// On trie par ordre chronologique
creneaux ← trierParOrdreChronologique(creneaux)
// On connaît le nombre de tests à effectuer
POUR position ALLANT DE 0 À nombreDeTestsAFaire - 1 PAR PAS DE 1 FAIRE
// Pour le 1er test on utilise debutJournee
SI (position = 0) ALORS
debut ← debutJournee
SINON
// Lors du test 2 il faut prendre la fin du créneau 1
debut ← lireHoraireFinDeCreneau(creneaux[position - 1])
FIN SI
// Pour le dernier test, il faut utiliser finJournee !
SI (position = nombreDeTestsAFaire - 1) ALORS
fin ← finJournee
SINON
fin ← lireHoraireDebutDeCreneau(creneaux[position])
FIN SI
SI (dureeTrou(debut, fin) >= 60) ALORS
afficherReponse(debut)
finDuProgramme
FIN SI
FIN POUR
FIN
Et voici maintenant la v4 qui intègre la phase de filtrage des superpositions en amont avant d’exécuter l’algorithme principal de détection d’un créneau disponible.
Les modifications apportées sont en gras :
ALGORITHME detecterCreneauDisponible-v4
// La variable input contient déjà les données d'entrée
// C'est un tableau dont chaque case contient une ligne du fichier d'entrée
VARIABLES globales
CHAINE: input[] // tableau de chaînes de caractères
VARIABLES
CHAINE: debutJournee, finJournee, debut, fin, creneaux[]
ENTIER: nombreCreneaux, nombreDeTestsAFaire, position
DEBUT
debutJournee ← "07:59"
finJournee ← "18:00"
// Sur la première ligne du fichier d'entrée on lit le nombre de créneaux
nombreCreneaux ← input[0]
// On récupère juste les créneaux pour les trier
// Soit les cases 1 à nombreCreneaux du tableau input
creneaux ← input[1..nombreCreneaux]
// On trie par ordre chronologique
creneaux ← trierParOrdreChronologique(creneaux)
// On filtre les créneaux superposés
creneaux ← filtrerSuperpositions(creneaux)
// Il faut calculer les N+1 tests après le filtrage
// en se basant sur la taille du tableau creneaux
nombreDeTestsAFaire ← tailleDuTableau(creneaux) + 1
// On connaît le nombre de tests à effectuer
POUR position ALLANT DE 0 À nombreDeTestsAFaire - 1 PAR PAS DE 1 FAIRE
// Pour le 1er test on utilise debutJournee
SI (position = 0) ALORS
debut ← debutJournee
SINON
// Lors du test 2 il faut prendre la fin du créneau 1
debut ← lireHoraireFinDeCreneau(creneaux[position - 1])
FIN SI
// Pour le dernier test, il faut utiliser finJournee !
SI (position = nombreDeTestsAFaire - 1) ALORS
fin ← finJournee
SINON
fin ← lireHoraireDebutDeCreneau(creneaux[position])
FIN SI
SI (dureeTrou(debut, fin) >= 60) ALORS
afficherReponse(debut) finDuProgramme
FIN SI
FIN POUR
FIN
Vous pouvez télécharger l’algorithme et une implémentation possible de celui-ci en JavaScript (fichiers detecterCreneauDisponibleV4.algo et detecterCreneauDisponibleV4.js).
Et voilà ! On a terminé le gros du travail pour cet exercice !
On est maintenant capable de gérer les cas particuliers de superpositions et les créneaux dans le désordre pour une journée donnée.
Qu’est-ce qu’il nous reste à faire ? Eh bien gérer tout ça pour une semaine complète !
Gérer une semaine complète de créneaux
Avant de commencer à gérer une semaine complète, réintroduisons déjà le numéro du jour qu’on avait retiré par souci de simplification.
Voici un nouveau fichier d’entrée d’exemple avec ce numéro du jour :
2
1 11:30-12:00
1 09:30-10:00
La bonne nouvelle c’est qu’on travaille enfin sur un fichier qui pourrait être un « vrai » fichier de test de notre algorithme pour l’exercice donné. On touche au but !
Il va falloir réussir à extraire de ces lignes un tableau qui contiendra la liste des créneaux du lundi pour pouvoir l’utiliser dans la suite de notre algorithme (le trier, filtrer les superpositions puis chercher un créneau disponible).
Je rappelle que les numéros du jour sont : 1 = lundi, 2 = mardi, … , 5 = vendredi.
Pour extraire les créneaux on peut écrire un petit algorithme très simple qui vient lire chaque ligne, en extraire le créneau et le stocker dans un tableau creneauxDuJour.
Par exemple :
ALGORITHME lireCreneauxDuJour
VARIABLES globales
CHAINE: input[]
VARIABLES locales
CHAINE: creneau, creneauxDuJour[]
ENTIER: nombreCreneaux, position
DEBUT
// Sur la première ligne du fichier d'entrée on lit le nombre de créneaux
nombreCreneaux ← input[0]
// On lit les créneaux à partir de la 2ème ligne d'input (indice 1)
POUR position ALLANT DE 1 À nombreCreneaux PAR PAS DE 1 FAIRE
// On extrait le créneau de la ligne contenant le numéro du jour
// et le créneau
creneau ← extraireCreneau(input[position])
// On ajoute ce créneau dans notre tableau final
ajouterDansTableau(creneauxDuJour, creneau)
FIN POUR
// À partir d'ici on peut exploiter creneauxDuJour
FIN
La fonction extraireCreneau permet de récupérer uniquement le créneau « 11:30-12:00 » de la ligne complète « 1 11:30-12:00 » par exemple.
Cet algorithme fonctionne pour un seul jour. Augmentons la difficulté et mettons un second jour dans notre fichier d’entrée :
4 1 11:30-12:00 2 10:45-13:30 2 09:15-15:00 1 09:30-10:00
L’objectif final de l’exercice, c’est d’afficher le créneau disponible avec son numéro du jour comme ceci : « <numeroJour> <creneauDisponible> ».
Il faut donc qu’on puisse tester tous les jours un par un et dès qu’on trouve un créneau de 60 minutes disponible, l’afficher et arrêter le programme.
Pour ça on pourrait décider de créer 5 tableaux lundi, mardi, mercredi, jeudi et vendredi qui contiendraient leurs créneaux respectifs et les tester un par un. Mais ce serait un petit peu laborieux à faire et on aurait beaucoup de code redondant.
Ce serait plus simple d’utiliser une boucle. Pour ça on va créer un tableau de tableaux, c’est-à-dire un tableau dont les valeurs sont des tableaux. On appelle ça un tableau à 2 dimensions.
Appelons ce tableau creneauxSemaine. Ce tableau contiendra 5 valeurs qui seront respectivement le tableau des créneaux du lundi, du mardi, du mercredi, du jeudi et du vendredi.
On déclare un tableau de tableaux en pseudo-code avec la notation creneauxSemaine[][]. Pour accéder au tableau de créneaux du lundi (1ère case) il suffira d’utiliser l’indice 0 dans le 1er crochet creneauxSemaine[0].
Pour accéder au 1er créneau du lundi, il suffira d’utiliser l’indice 0 dans le 2ème crochet creneauxSemaine[0][0]. Pour accéder au 2ème créneau du lundi il suffira d’utiliser creneauxSemaine[0][1].
Dernier exemple : pour accéder au 3ème créneau du mardi il faudra appeler creneauxSemaine[1][2]. Souvenez-vous qu’on compte à partir de 0 dans les tableaux. Donc le 3ème créneau est dans la case 2 (dans la case d’indice 2).
Autrement dit on l’utilise comme ça : creneauxSemaine[<indice-du-jour>][<indice-du-créneau>].
Attention petit point à noter le numéro du lundi est 1 mais l’indice du jour du lundi pour notre tableau creneauxSemaine est 0 car on compte à partir de zéro.
Donc il faudra penser à soustraire 1 au numéro du jour pour obtenir l’indice du jour pour faire l’appel creneauxSemaine[<indice-du-jour>] avec le bon indice !
En utilisant cet algorithme on va pouvoir facilement trier toutes les lignes du fichier d’entrée et stocker le tout dans un tableau.
Voici une proposition possible :
ALGORITHME lireCreneauxSemaine
VARIABLES globales
CHAINE: input[]
VARIABLES locales
CHAINE: creneau, creneauxSemaine[][]
ENTIER: nombreCreneaux, position, numeroDuJour, indiceDuJour
DEBUT
// Sur la première ligne du fichier d'entrée on lit le nombre de créneaux
nombreCreneaux ← input[0]
// On lit les créneaux à partir de la 2ème ligne d'input (indice 1)
POUR position ALLANT DE 1 À nombreCreneaux PAR PAS DE 1 FAIRE
// On extrait le numéro du jour qu'on utilisera comme indice
numeroDuJour ← extraireNumeroJour(input[position])
// On extrait le créneau
creneau ← extraireCreneau(input[position])
// On n'oublie pas de soustraire 1 au numéro du jour pour obtenir
// le bon indice
indiceDuJour ← numeroDuJour - 1
// On ajoute ce créneau dans la bonne case correspondant à son jour
ajouterDansTableau(creneauxSemaine[indiceDuJour], creneau)
FIN POUR
FIN
Vous pouvez télécharger l’algorithme et une implémentation possible de celui-ci en JavaScript (fichiers lireCreneauxSemaine.algo et lireCreneauxSemaine.js).
La nouvelle fonction extraireNumeroJour permet de récupérer le numéro du jour « 1 » de la ligne complète « 1 11:30-12:00 » par exemple.
Et voilà ! On a maintenant dans chaque case du tableau creneauxSemaine la liste des créneaux de chaque jour présent dans notre fichier d’entrée.
Il ne reste plus qu’à intégrer cette partie dans l’algorithme final qu’on va passer en v5 !
Comme d’habitude, je rappelle la version 4 ici et mets en dessous la v5.
ALGORITHME detecterCreneauDisponible-v4
// La variable input contient déjà les données d'entrée
// C'est un tableau dont chaque case contient une ligne du fichier d'entrée
VARIABLES globales
CHAINE: input[] // tableau de chaînes de caractères
VARIABLES
CHAINE: debutJournee, finJournee, debut, fin, creneaux[]
ENTIER: nombreCreneaux, nombreDeTestsAFaire, position
DEBUT
debutJournee ← "08:00"
finJournee ← "17:59"
// Sur la première ligne du fichier d'entrée on lit le nombre de créneaux
nombreCreneaux ← input[0]
// On récupère juste les créneaux pour les trier
// Soit les cases 1 à nombreCreneaux du tableau input
creneaux ← input[1..nombreCreneaux]
// On trie par ordre chronologique
creneaux ← trierParOrdreChronologique(creneaux)
// On filtre les créneaux superposés
creneaux ← filtrerSuperpositions(creneaux)
// Il faut calculer les N+1 tests après le filtrage
nombreDeTestsAFaire ← tailleDuTableau(creneaux) + 1
// On connaît le nombre de tests à effectuer
POUR position ALLANT DE 0 À nombreDeTestsAFaire - 1 PAR PAS DE 1 FAIRE
// Pour le 1er test on utilise debutJournee
SI (position = 0) ALORS
debut ← debutJournee
SINON
// Lors du test 2 il faut prendre la fin du créneau 1
debut ← lireHoraireFinDeCreneau(creneaux[position - 1])
FIN SI
// Pour le dernier test, il faut utiliser finJournee !
SI (position = nombreDeTestsAFaire - 1) ALORS
fin ← finJournee
SINON
fin ← lireHoraireDebutDeCreneau(creneaux[position])
FIN SI
SI (dureeTrou(debut, fin) >= 60) ALORS
afficherReponse(debut)
finDuProgramme
FIN SI
FIN POUR
FIN
Ci-dessous la v5 qui intègre maintenant la gestion des numéros du jour et la création du tableau creneauxSemaine.
Il faut créer une boucle qui va parcourir chaque jour et chercher un créneau disponible dans celui-ci.
Les points de modifications importants à noter (bogues que j’ai rencontrés et corrigés via des itérations) :
- Un jour donné peut n’avoir aucun créneau, auquel cas, on ne le traitera pas
afficherResultatdoit prendre en paramètre le numéro du jour pour pouvoir l’afficher !
ALGORITHME detecterCreneauDisponible-v5
// La variable input contient déjà les données d'entrée
// C'est un tableau dont chaque case contient une ligne du fichier d'entrée
VARIABLES globales
CHAINE: input[] // tableau de chaînes de caractères
VARIABLES
CHAINE: debutJournee, finJournee, debut, fin, creneauxSemaine[][]
ENTIER: nombreCreneaux, nombreDeTestsAFaire, position, indiceDuJour
DEBUT
debutJournee ← "07:59"
finJournee ← "18:00"
// Sur la première ligne du fichier d'entrée on lit le nombre de créneaux
nombreCreneaux ← input[0]
// On lit les créneaux à partir de la 2ème ligne d'input (indice 1)
POUR position ALLANT DE 1 À nombreCreneaux PAR PAS DE 1 FAIRE
// On extrait le numéro du jour qu'on utilisera comme indice
numeroDuJour ← extraireNumeroJour(input[position])
// On extrait le créneau
creneau ← extraireCreneau(input[position])
// On n'oublie pas de soustraire 1 au numéro du jour pour obtenir
// le bon indice
indiceDuJour ← numeroDuJour - 1
// On ajoute ce créneau dans la bonne case correspondant à son jour
ajouterDansTableau(creneauxSemaine[indiceDuJour], creneau)
FIN POUR
// On lit les créneaux de chaque jour dans notre tableau creneauxSemaine
POUR indiceDuJour ALLANT DE 0 À tailleDuTableau(creneauxSemaine) - 1 PAR PAS DE 1 FAIRE
creneaux ← creneauxSemaine[indiceDuJour];
// On ne traite que les jours avec des créneaux
SI (tailleDuTableau(creneaux) > 0) ALORS
// On trie par ordre chronologique
creneaux ← trierParOrdreChronologique(creneaux)
// On filtre les créneaux superposés
creneaux ← filtrerSuperpositions(creneaux)
// Il faut calculer les N+1 tests après le filtrage
nombreDeTestsAFaire ← tailleDuTableau(creneaux) + 1
// On connaît le nombre de tests à effectuer
POUR position ALLANT DE 0 À nombreDeTestsAFaire - 1 PAR PAS DE 1 FAIRE
// Pour le 1er test on utilise debutJournee
SI (position = 0) ALORS
debut ← debutJournee
SINON
// Lors du test 2 il faut prendre la fin du créneau 1
debut ← lireHoraireFinDeCreneau(creneaux[position - 1])
FIN SI
// Pour le dernier test, il faut utiliser finJournee !
SI (position = nombreDeTestsAFaire - 1) ALORS
fin ← finJournee
SINON
fin ← lireHoraireDebutDeCreneau(creneaux[position])
FIN SI
SI (dureeTrou(debut, fin) >= 60) ALORS
afficherReponse(indiceDuJour, debut)
finDuProgramme
FIN SI
FIN POUR
FIN SI
FIN POUR
FIN
Vous pouvez télécharger l’algorithme et une implémentation possible de celui-ci en JavaScript (fichiers detecterCreneauDisponibleV5.algo et detecterCreneauDisponibleV5.js).
Et c’est terminé !
Ce dernier algorithme en version 5 répond à l’énoncé et passe tous les tests sur le site isograd. Vous pouvez utiliser le fichier detecterCreneauDisponibleV5.js et copier tout le code de la fonction detecterCreneauDisponible-v5 dans la fonction ContestResponse() dans l’éditeur de code du site isograd et ça va fonctionner !
Bravo d’avoir lu jusqu’ici 👏.
La méthode pour rédiger un algorithme
Voici la méthode et les différentes étapes à suivre que vous pourrez appliquer à n’importe quel problème à résoudre :
- Simplifiez le problème jusqu’à son cœur sans en modifier la nature
- Explorez ce problème avec des exemples simples pour vous l’approprier
- Utilisez la règle des 3 possibilités pour trouver les cas particuliers
- Résolvez ce problème et les cas particuliers
- Itérez : ajouter une difficulté supplémentaire puis résolvez ce nouveau problème
- Vérifiez que votre nouvel algorithme fonctionne toujours pour le problème précédent
- Répétez ces étapes jusqu’à obtenir toutes les difficultés du problème initial
- Félicitations vous avez maintenant une solution au problème donné !
Gardez en tête qu’il ne faut pas entrer dans les détails quand vous rédigez un algorithme en pseudo-code, gardez une vision assez « haute » du problème que vous essayez de résoudre.
Vous écrirez les fonctionnalités de « bas niveau » nécessaires plus tard.
Souvenez-vous aussi qu’un exercice complexe n’est au final qu’un enchaînement de sous-problèmes à résoudre. Isolez ces problèmes un par un, adressez-les et vous réussirez à résoudre n’importe quel exercice difficile !
Une question de temps et d’itération
J’aimerai à nouveau rappeler que cet article se lit de façon linéaire mais que la construction d’un algorithme ne l’est jamais. Je n’ai pas arrêté de faire des va-et-viens entre mon code et mon algorithme pour l’écrire correctement.
Presque quasiment à chaque fois, j’ai fait au moins une erreur sur un algorithme ! Que ce soit une erreur de logique ou d’implémentation. Même après 10 ans d’expérience on fait des erreurs, c’est normal.
C’est impossible de rédiger l’intégralité d’un tel algorithme de façon linéaire et du premier coup. C’est pour ça qu’on procède par itérations.
J’ai mis 3 semaines à mi-temps pour rédiger cet article. Je le voulais complet et abordable pour des débutants, j’espère avoir réussi mon pari (dites-moi dans les commentaires !).
Je tenais à vous préciser qu’il ne faut pas autant de temps pour rédiger un tel algorithme, en quelques heures ou quelques minutes pour les plus chevronnés on peut en venir à bout avec de l’expérience.
Toutes les réflexions que j’ai décrites longuement dans cet article se font en quelques secondes ou millisecondes dans le cerveau.
Par ailleurs, une fois qu’on a l’habitude, on passe directement de la phase algorithme dans la tête à la phase de rédaction du programme dans le langage de programmation de son choix.
On ne rédige plus les algorithmes avec du pseudo-code avant de les coder, on les code directement. C’est ce qui vous donne l’impression que les développeurs ne passent pas par cette phase de création d’un algorithme : mais c’est faux !
Il y passent mais ils font tout directement dans la mémoire de leur cerveau. J’espère avoir rétabli un peu de vérité sur ce qui se passe vraiment dans le cerveau d’un développeur avec cet article 😁.
Le mot de la fin
Je le dis à nouveau tout le code que j’ai écrit est adapté pour les débutants, je sais qu’on peut le rédiger de façon bien plus compacte et moderne en JavaScript mais ce n’est pas le but de ce code !
Par ailleurs, les choix faits pour la rédaction des algorithmes sont eux aussi adaptés pour les débutants, j’ai souhaité rester sur des techniques de base classiques et décortiquer chaque étape dans le détail.
Je sais qu’il existe de nombreuses façons de faire différemment, mieux, plus optimisé etc. mais à nouveau, l’objectif ici est d’amener une pédagogie et une structure pour aider les débutants à comprendre les étapes qu’on fait dans notre cerveau pour arriver à une solution sur un tel exercice.
Conclusion
J’espère avoir pu décortiquer avec un niveau de détails suffisant ma réflexion pour résoudre cet exercice et vous avoir redonné foi dans vos capacités à résoudre des exercices de plus en plus complexes.
L’objectif ici est de vous donner la méthode que j’utilise pour résoudre n’importe quel exercice complexe pour que vous puissiez l’utiliser. Armé de cette méthode vous pourrez maintenant aborder n’importe quel problème sereinement.
Prenez votre temps pour rédiger des réponses aux exercices, ne regardez pas les solutions trop vite où vous n’apprendrez rien ! Au début ça vient lentement, il faut plusieurs heures pour résoudre un exercice simple, c’est normal.
Plus vous allez pratiquer et plus ce sera facile et vous irez vite !
Si vous avez apprécié la qualité de mon travail sur cet article gratuit j’aimerai vous solliciter pour en parler autour de vous sur les réseaux sociaux. Prenez le temps de le partager pour le faire connaître à un ami débutant en programmation ou même à vos amis développeurs !
Vous pouvez le partager sur Twitter où je suis très présent en cliquant sur ce lien. Merci d’avance pour votre soutien 👍.
Si vous voulez aller plus loin en algorithmique, vous pouvez suivre le module algorithmique de ma formation JavaScript.
J’espère vous y voir très bientôt !
PS : Si vous trouvez des erreurs, merci de me contacter via les commentaires ou sur Twitter pour m’en faire part que je les corrige. Merci beaucoup !
Amicalement,
Jérémy.
« Les minutes de début et de fin sont incluses dans l’horaire donc une réunion de 08:00 à 08:59 ou de 09:20 à 10:19 fait exactement 60 minutes »
Même si on compte concrètement 59 minutes mais que l’énoncé dit que c’est 60 minutes, il faut faire abstraction de ce que l’on constate et prendre ce que l’on nous donne sans se poser de questions ?
Car moi, dès le début, j’aurai compté 30 minutes et pas 31 minutes entre 8h et 8h30, et j’aurai bloqué sans comprendre pourquoi parce que c’est juste logique dans ma tête 🙁
Oui c’est l’énoncé qui dicte les règles à appliquer (qu’on appelle les spécifications du problème), que ça nous semble logique ou pas on doit se plier aux règles de l’énoncé pour fournir la bonne solution à cet exercice.
C’est super !!!
Un grand merci et un grand bravo Jeremy pour cette vaste article qui m’a été très utile.
Merci Jérémy…Ton travail m’a vraiment permis de reprendre confiance en mes capacité,de voir les erreurs que je commets régulièrement et puis de constater que certains sont normals.Merci beaucoup
lorsque tu disais qu’il faut lire à plusieurs reprises cet article,tu as vraiment raison parce que c’est après l’avoir fait que j’ai pu constater que pour simplifier le problème d’un exercice de programmation,il faut :
-Noter les points importants de celui-ci
-Analyser ces derniers un à un
-Dans l’analyse,tester chacun d’eux avec des exemples et en tirer des éventuels conclusions
-Analyser un exemple qui illustre le problème global de l’énoncé
-Identifier le ou les cas particuliers qui ressortent de cet exemple
-Identifier ensuite progressivement les difficultés liés au problème
-Puis enfin retirer les difficultés jusqu’à atteindre le coeur du problème
Je le met au cas ou des gens aurait eu les mêmes problèmes à identifier les étapes de simplification du problème et au cas ou d’autres auraient des choses à ajouter ou à en retirer.
« l’horaire de début et de fin de créneau ne peuvent pas être égaux (ça n’aurait pas de sens d’avoir un créneau de 0 min !) »
Sachant que dureeCreneau = horaireDeFin – horaireDeDebut + 1, un créneau avec des horaires de début et de fin identiques a donc une durée de 1 min, ce qui est un cas limite mais a priori parfaitement admissible 😉
Oui tout à fait, je parlais plus d’un point de vue général mais avec l’énoncé précis c’est en effet un cas possible !
Bonjour,
super article, que je commence à lire mais par contre je comprends pas pour les 31 mn 8h 8h30 parceque un rendez vous de 8:00 à 8:30 il fait bien 30mn, et non pas 31mn, on parle du début de la minute, càd 8:00:00 à 08:30:00 et non pas jusqu’à 8:30:59 où ca ferait un rendez vous de 30mn et 59 secondes. Si tu chronomètre sur une horloge entre l’affichage de 13h et 13:10 il y a bien 10mn.
Comme le dit Guillaume sinon tu peux pas avoir de rendez vous de 1 mn, ou alors il commence à 8:00 et se finit à 8:00 selon le mode de calcul utilisé dans l’article.
C’est comme les 35 heures tu fais 7 heure par jour 8h 16h avec une heure le midi ! 🙂
Bonjour, il n’y a rien à comprendre, c’est l’énoncé qui impose la règle de compter les durées comme ça !
Moi aussi ça m’a perturbé mais on doit se plier aux contraintes de l’énoncé.
Et oui un rdv qui commencerait à 08:00 et se terminerait à 08:00 ferait 1 minute selon les contraintes de l’énoncé.
Ça ne semble pas spécialement logique mais à nouveau, ce n’est pas à nous d’en décider, c’est l’énoncé qui dicte les règles et il faut les suivre.
Gé-nial !
merci grâce a toi j’entrevois ce qu’est le problem solving, mon point d’entree dans le monde du dev !!
j’en veux encore !!
as tu des fiches expliquant la resolution d’autres problemes s’il te plait?
en tout cas merci bcp.
Salut Donei, merci pour ton message ! J’ai un module de formation complet à ce sujet : le module algorithmique.
Cet article aide beaucoup puisque toute programmation, quel que soit le langage qu’on va utiliser dans la réalisation d’un programme, comprendre l’algorithme est primordial.
Une fois qu’on comprend bien l’algorithme, l’apprentissage d’un ou plusieurs langages de programmation devient plus facile.
Merci